
Der Begriff der Entropie gilt manchmal als schwierig und unanschaulich. Ein Grund dafür ist sicher, dass man in der klassischen Thermodynamik die Entropie gleichsam hinten herum über die Wärmemenge einführt, und dass man so ihre wahre Natur nicht erfassen kann. Ein weiterer Grund ist vielleicht, dass Entropie in der Physik keine Erhaltungsgröße ist, anders als beispielsweise die Energie. Die Entropie nimmt von sich aus zu, wenn sich ein System auf das thermische Gleichgewicht zubewegt.
Man kann die Entropie aber sehr wohl anschaulich einführen, wenn man von der inneren Natur der Materie (Teilchen und Quanten) ausgeht. So wird die Entropie zum grundlegenden statistischen Begriff der Thermodynamik und erhält zugleich von Anfang an eine anschauliche Bedeutung. Sie bildet dann die Basis, um weitere Begriffe wie beispielsweise die Temperatur präzise zu definieren. Diesen Weg wollen wir hier gehen. Um Sie, lieber Leser, nicht zu sehr mit Vorbereitungen auf die Folter zu spannen, ist hier ohne weitere Umschweife die wesentliche Kernidee:
|
Die anschauliche Bedeutung der Entropie: Wie viele Möglichkeiten haben die Gasteilchen in einem Gasbehälter, um im Mittel ein bestimmtes großräumiges Erscheinungsbild zu realisiseren, beispielsweise eine bestimmte räumliche Dichteverteilung? Sie haben extrem viele Möglichkeiten dafür! Typisch wäre eine Zahl wie \( 10^{ (10^{20} )} \). Um diese Zahl hinzuschreiben, braucht man etwa \( 10^{20} \) Dezimalstellen, die Zahl ist also Lichtjahre lang. Die Entropie für das betrachtete großräumige Erscheinungsbild ist nun gerade diese Anzahl Dezimalstellen, also gleichsam die Länge der Zahl an Möglichkeiten, das großräumige Erscheinungsbild im Detail zu realisieren. Meist versieht man dabei die Entropie zusätzlich noch mit einem Vorfaktor, um handhabbare Entropiewerte und bestimmte phsyikalische Einheiten für die Entropie zu erhalten. |

Diese Idee wollen wir nun präzisiseren und sehen, wie sich mit ihr die
gesamte klassische Thermodynamik begründen lässt. Wir werden verstehen können,
was Wärme, Temperatur oder Druck eigentlich sind, und warum bestimmte Prozesse
(z.B. chemische Reaktionen) einem bestimmten Gleichgewichtszustand zustreben.
Oben war von Möglichkeiten und einem bestimmten großräumigen Erscheinungsbild die Rede. Um die üblichen Begriffe zu verwenden, nennen wir das großräumige Erscheinungsbild Makrozustand und bezeichnen jede der einzelnen Möglichkeiten, diesen Makrozustand mikroskopisch zu realisieren, als Mikrozustand:
|
Mikro- und Makrozustände:
|
Natürlich ist es kaum möglich, die exakte Wellenfunktion eines makroskopischen Objektes
und damit seinen Mikrozustand exakt zu messen,
sobald dieser auch nur einige Dutzend Teilchen enthält. Bei der typischen Größenordnung
von \(10^{20}\) und mehr Teilchen ist es vollkommen illusorisch, den
Mikrozustand festzulegen, zumal das Objekt ständig im Kontakt mit seiner Umgebung ist
und sich der Mikrozustand daher ständig ändert
(selbst im leeren Weltraum würde ein Objekt Wärmestrahlung aussenden und absorbieren).
Das ist der Grund dafür, jeweils viele Mikrozustände statistisch zu einem Makrozustand zusammenzufassen, den man dann durch geeignete statistische Zustandsgrößen charakterisieren kann. So interessiert der Mikrozustand eines Steines normalerweise nicht, wohl aber seine Temperatur.
Damit ist auch klar, was man mit makroskopischem System meint: ein System, das extrem viele Mikrozustände besitzt und bei dem es Sinn macht, jeweils sehr viele dieser Mikrozustände zu Makrozuständen zusammenzufassen.
Wir werden noch sehen, dass die Zahl der Mikrozustände exponentiell mit der Zahl der Teilchen (bzw. allgemeiner der Freiheitsgrade) eines Systems anwächst, und dass ihr energetischer Abstand genauso schnell exponentiell schrumpft. Man hat es daher meist mit einem energetischen Quasi-Kontinuum von Mikrozuständen zu tun.
Die Zahl der Mikrozustände übersteigt selbst bei relativ wenigen Teilchen (sagen wir, einigen Tausend) schnell die Zahl der Atome im sichtbaren Universum (diese beträgt weniger als \(10^{100}\), siehe Wikipedia: Universum). Bei der typischen Zahl von \(10^{20}\) und mehr Teilchen für makroskopische Körper wird die Zahl der Mikrozustände unvorstellbar groß – man denke an Zahlen wie \( 10^{ (10^{20} )} \). Das sieht harmlos aus, aber wenn man diese Zahl ausschreibt und pro Dezimalstelle etwa 5 mm Platz braucht, dann ist die ausgeschriebene Zahl \(5 \cdot 10^{14}\) km lang – das sind etwa 50 Lichtjahre, also mehr als 10 mal weiter als bis zum nächsten Stern. So lang wäre die ausgeschriebene Zahl der Mikrozustände.
Wir hatten die Anzahl der Mikrozustände, die ein Makrozustand umfasst, oben bereits mit \( \Omega \) bezeichnet. Genau genommen müsste man so etwas wie \( \Omega(A, B, C, \, ...) \) schreiben, wobei \(A, B, C\) usw. die Zustandsgrößen sind, die den Makrozustand festlegen – beispielsweise Energie, Volumen und Teilchenzahl.
Da \( \Omega \) meist eine extrem große Zahl ist, bietet es sich an, nicht direkt mit \(\Omega\) zu arbeiten, sondern mit dem Logarithmus von \(\Omega\).
Der Logarithmus hat den Vorteil, dass Produkte von \(\Omega\)'s zu Summen der Logarithmen werden, beispielsweise wenn man zwei Systeme zu einem Gesamtsystem zusammensetzt.
Bei großen Zahlen kann man sagen: Der Logarithmus misst, wie viele Stellen man braucht, um die Zahl aufzuschreiben. Zumindest wäre das beim Zehnerlogarithmus so.
Üblicherweise verwendet man aber den natürlichen Logarithmus, der sich vom Zehnerlogarithmus nur ungefähr um einen Vorfaktor 2,3 unterscheidet, und fügt aus historischen Gründen noch einen weiteren Vorfaktor hinzu: die Boltzmannkonstante \begin{align} k &= 1,38 \, ... \cdot 10^{- 23} \frac{\mathrm{J}}{\mathrm{K}} = \\ &= 8,617 \, ... \cdot 10^{- 5} \frac{\mathrm{eV}}{\mathrm{K}} \end{align} Wenn in einem Makrozustand alle Mikrozustände mit gleicher Wahrscheinlichkeit auftreten, so bezeichnet man den natürlichen Logarithmus von \( \Omega \) zusammen mit dem Vorfaktor als Entropie \(S\) des Makrozustandes. Das ist für ein makroskopisch abgeschlossenes System im thermischen Gleichgewicht der Fall, wie wir noch sehen werden.
Der Grund für den Vorfaktor \(k\) liegt darin, dass man die Temperatur später in der gewohnten Einheit Kelvin angeben möchte, was dazu führt, dass die Entropie die Dimension Energie pro Temperatur hat. Das war historisch die natürliche Dimension der Entropie bei ihrer klassischen Definition über die quasistatische Wärmeübertragung bei fester Temperatur (siehe unten). Fassen wir zusammen:
|
Entropie: Treten die erreichbaren Mikrozustände eines Makrozustandes mit gleicher Wahrscheinlichkeit auf, so ist die Entropie \(S\) dieses Makrozustandes proportional zum natürlichen Logarithmus der Anzahl \( \Omega \) dieser Mikrozustände definiert. Als Proportionalitätsfaktor wählt man üblicherweise die Boltzmannkonstante \begin{align} k &= 1,38 \, ... \cdot 10^{- 23} \frac{\mathrm{J}}{\mathrm{K}} = \\ &= 8,617 \, ... \cdot 10^{- 5} \frac{\mathrm{eV}}{\mathrm{K}} \end{align} Es ist also \[ S := k \, \ln{\Omega} \] Die Entropie ist damit ungefähr proportional zur Anzahl Dezimalstellen, die man benötigt, um die riesige Anzahl \(\Omega\) der Mikrozustände aufzuschreiben ( \( \ln{\Omega} \) ist ungefähr 2,3 mal die Dezimalstellenanzahl von \(\Omega\) ). Weiter unten werden wir die Definition noch für den Fall verallgemeinern, dass die Mikrozustände mit unterschiedlicher Wahrscheinlichkeit auftreten.
|
Wie groß ist die kleinste mögliche Entropie?
Die Formel oben zeigt sofort: Null ist der kleinstmögliche Wert für Entropie
(dritter Hauptsatz der Thermodynamik).
Dieser Fall tritt ein, wenn der Makrozustand nur einen einzigen Mikrozustand umfasst, denn \(\ln{1} = 0 \)
(man müsste also beim Zählen der Dezimalstellen wohl mit einer nullten Stelle anfangen).
Das geschieht beispielsweise, wenn man einem Festkörper jede thermische Energie entzieht,
so dass er in den quantenmechanischen Grundzustand übergeht
(siehe beispielsweise das Phänomen der Bose-Einstein-Kondensation weiter unten).
Übrigens: Definiert man den Entropiebegriff auf Basis der klassichen Mechanik statt der Quantenmechanik, so gibt es keine gut definierten Mikrozustände und damit auch keinen Grundzustand. Die Entropie ist dann nur bis auf eine beliebige additive Konstante bestimmt. An die Stelle der Mikrozustände tritt das sogenannte Phasenraumvolumen, das man in kleine Parzellen aufteilt, wobei die Größe dieser Parzellen einmalig beliebig festgelegt werden kann. Die Zahl der Parzellen im erreichbaren Phasenraumvolumen entspricht dann der Zahl der Mikrozustände. Hier kann man nur sinnvoll von Entropiedifferenzen sprechen, aber nicht vom absoluten Wert der Entropie, denn eine andere Festlegung der Parzellengröße führt zu einer anderen additiven Konstante bei der Entropie. Wir verfolgen diesen etwas veralteten Ansatz hier nicht, denn wir wissen ja, dass die Quantenmechanik die fundamentalere Theorie ist.
Ja – und das wäre es eigentlich schon! Die Definition ist also im Grunde ganz einfach. Nun müssen wir nur noch herausfinden, was sie in verschiedenen Zusammenhängen bedeutet, insbesondere in der Physik makroskopischer Systeme.
Oft verbindet man große Entropie mit großer Unordnung. Das kann hilfreich, aber auch verwirrend sein. Zudem ist der Begriff Unordnung eher intuitiv und nicht sonderlich präzise definiert.
Wenn es nur relativ wenige Mikrozustände gibt, die wir als geordnet ansehen würden, dann ist die Verknüpfung von Entropie und Unordnung hilfreich. Das typische Beispiel ist die unaufgeräumte Wohnung: Hier gibt es sehr viel mehr Möglichkeiten, die persönlichen Habseligkeiten unordentlich in der Wohnung zu verteilen, als sie ordentlich aufzubewahren. In diesem Sinne hat der Makrozustand unaufgeräumte Wohnung sehr viel mehr Mikrozustände als der Makrozustand aufgeräumte Wohnung.
Es kann aber auch Fälle geben, bei denen wir die meisten Mikrozustände als geordnet ansehen würden – dann ist die Verknüpfung unglücklich. Ein Beispiel ist die Beschreibung von Materie und Gravitation in der allgemeinen Relativitätstheorie mit Berücksichtigung von Quanteneffekten. Ein schwarzes Loch hat hier eine große Entropie, und tatsächlich neigt hinreichend kalte Materie ja durchaus dazu, aufgrund der Gravitation zu verklumpen und ggf. schwarze Löcher zu bilden. Würden wir schwarze Löcher intuitiv als ungeordnet empfinden?
Ein anderes Beispiel ist das spontane Entstehen von Ordnung, wenn wenige große Teilchen (z.B. große organische Moleküle) in einem Meer kleiner Teilchen schwimmen. Die großen Teilchen haben hier häufig die Tendenz, sich eng zusammenzufinden, da so mehr Platz für die Bewegung der kleinen Teilchen entsteht, was in Summe die Gesamtentropie erhöht. Dabei können die großen Teilchen sogar spontan geordnete Strukturen bilden, wenn dies mehr Platz für die kleinen Teilchen schafft – Entropie schafft hier also Ordnung statt Unordnung! Allerdings beachten wir dabei nur die zunehmende Ordnung (abnehmende Entropie) der großen Teilchen, während uns die erweiterten Bewegungsmöglichkeiten (stark zunehmende Entropie) der kleinen Teilchen nicht weiter interessieren. Solche Prozesse scheinen in der Biochemie lebender Zellen eine nicht unwichtige Rolle zu spielen. Mehr dazu siehe beispielsweise in Peter Weiß: Another Face of Entropy – Particles self-organize to make room for randomness, auch hier zu finden.
Statt unordentlich ist der Begriff makroskopisch informationsarm für einen Makrozustand hoher Entropie besser. Ein noch-so-großes schwarzes Loch lässt sich beispielsweise durch nur drei(!) Kenngrößen vollständig beschreiben: Masse, Drehimpuls und Elektrische Ladung (siehe Wikipedia: Schwarzes Loch). Entsprechend enthüllt der Makrozustand eines schwarzen Lochs nur sehr wenig Information. Schwarze Löcher haben sogar eine Entropie und eine Temperatur – mehr dazu in Kapitel 3.
Wachsende Entropie hat also etwas mit wachsender Zufälligkeit auf der Mikro-Ebene und Informationsverlust auf der Makro-Ebene zu tun, denn immer mehr Mikrozustände können statistisch durch denselben Makrozustand beschrieben werden, für den man nur wenige Zustandsgrößen braucht. Wir werden in Kapitel 2 noch einmal im Detail auf den engen Zusammenhang zwischen Entropie und Information zurückkommen.
Wie groß sind typische Entropien für Objekte in unserer täglichen Umgebung? Typische Werte bei Zimmertemperatur und Atmosphärendruck bewegen sich zwischen 50 und 300 Joule pro Kelvin und Mol. Die höchsten Entropiewerte haben Gase, die niedrigsten Festkörper, und zwar umso weniger, je stärker die Atome aneinander gebunden sind (siehe z.B. Thermodynamics of chemical equilibrium: What is entropy?).
Division durch die Boltzmannkonstante ergibt für \( \ln{\Omega} \) Werte von der Größenordnung \( 10^{25} \) für ein Mol (etwa \( 6 \cdot 10^{23} \) Teilchen, beispielsweise 2 Gramm Wasserstoff oder 12 Gramm Kohlenstoff).
Die Zahl der Mikrozustände pro Makrozustand ist demnach ungefähr \( \Omega = 2,718^{ (10^{25} )} \), ist also von der Größenordnung \( 10^{ (10^{24} )} \) für etwa \(10^{23}\) Teilchen bei Zimmertemperatur. Das sind genau die extrem großen Zahlen, die wir oben erwähnt hatten. Also:
|
Typische Entropien: Bei Zimmertemperatur (300 K) und Atmosphärendruck liegt die typische Entropie von einem Mol Teilchen (etwa \( 6 \cdot 10^{23} \) Teilchen) bei \[ S = 50 \; \mathrm{bis} \; 300 \frac{J}{K} \] Die entsprechende Anzahl Mikrozustände pro Makrozustand liegt bei der Größenordnung: \[ \Omega \approx 10^{ (10^{24} )} \] |
Ist es Ihnen aufgefallen? Die Entropie ist ja immer für einen Makrozustand
definiert. Wo ist der Makrozustand? Offenbar reicht es im Wesentlichen, die
Temperatur, die Stoffmenge und Stoffart sowie den Druck (oder das Volumen) anzugeben,
um den Makrozustand zu spezifizieren. Warum das so ist, kommt später.
Der entscheidende Schritt bei der Definition der Entropie war: Man fasst viele Mikrozustände geeignet zu Makrozuständen zusammen. Dabei wird es Makrozustände geben, die sehr viel mehr Mikrozustände umfassen als andere Makrozustände. Was bedeutet das?
Schauen wir uns dazu ein System an, das makroskopisch abgeschlossen ist, d.h. es soll nur sehr wenig mit seiner Umgebung in Wechselwirkung stehen (ganz vermeiden kann man das bei makroskopischen Systemen ja nie). Ein Beispiel für ein solches System wäre ein gefüllter Gasbehälter mit einer sehr guten thermischer Isolierung.
Nehmen wir nun an, wir starten mit einem Makrozustand, der nur einen kleinen Teil der Mikrozustände umfasst, die für das System prinzipiell unter den gegebenen Randbedingungen erreichbar sind. Beispielsweise könnten wir einen Gasbehälter betrachten, bei dem sich alle Gasteilchen in der rechten Hälfte befinden. Nun überlassen wir das System sich selbst. Das System wird beginnen, sich zufällig im Raum der erreichbaren Mikrozustände zu bewegen, denn bei einem makroskopischen System ist ein Mikrozustand nicht stabil – das System unterliegt unvermeidlich winzigen äußeren Einflüssen, die es sehr schnell von einem Mikrozustand zum nächsten springen lassen. Man kann sich vorstellen, dass sich das System auf einem Zufallspfad im Raum der erreichbaren Mikrozustände bewegt.
Jede Messung am System braucht nun eine gewisse Zeit, so dass man bei dieser Messung immer einen Mittelwert über viele Mikrozustände erhält. Eine andere Interpretation ist die, dass sich ein makroskopisches Quantensystem sowieso nie komplett in einem einzigen Quantenzustand (Mikrozustand) befindet – dafür müsste man diesen Zustand ja durch Messung erst präparieren, was hoffnungslos ist. Man beschreibt solche Quantensysteme durch eine quantenmechanische Dichtematrix, also durch ein klassisch-statistisches Gemisch von Quantenzuständen (zur Dichtematrix siehe den Anhang weiter unten sowie Die Symmetrie der Naturgesetze, Kapitel 4.5). Hier ist die Mittelung über viele Mikrozustände schon von Anfang an eingebaut.
Auf dem Zufallsweg durch die erreichbaren Mikrozustände wird das System irgendwann die Mikrozustände verlassen, die zu dem Anfangs-Makrozustand gehören, denn dieser Anfangs-Makrozustand umfasst ja nur einen kleinen Teil der erreichbaren Mikrozustände. Die Gasteilchen werden sich im Gasbehälter verteilen. Da wir davon ausgehen, dass bei einem abgeschlossenen System auf Dauer kein erreichbarer Mikrozustand bevorzugt wird, werden alle erreichbaren Mikrozustände im Lauf der Zeit gleich wahrscheinlich werden, also während der Messzeit gleich häufig auftreten (das ist die statistische Grundannahme für ein abgeschlossenes System). Die Wahrscheinlichkeiten werden damit zugleich auch zeitlich konstant.
Sobald dies eingetreten ist, spricht man von thermischen Gleichgewicht. Wie lange es dauert, bis das thermische Gleichgewicht erreicht ist, kann sehr unterschiedlich sein – es kann Millisekunden oder Jahre dauern. Die Annäherung an das Gleichgewicht erfolgt umgekehrt exponentiell, also erst schneller und dann immer langsamer. Die typische Zeitskala bezeichnet man dabei als Relaxationszeit.
Zum thermischen Gleichgewicht gehört bei einem makroskopischen Körper automatisch das mechanische Gleichgewicht dazu. Das bedeutet, dass sich äußere Parameter wie das Volumen nicht mehr ändern dürfen – die Energieniveaus der Mikrozustände müssen konstant bleiben (mehr dazu gleich). Im Allgemeinen stellt sich das mechanische Gleichgewicht sehr viel schneller ein als das thermische Gleichgewicht (Drücke gleichen sich meist schneller aus als Temperaturen).
Ein Makrozustand mit vielen erreichbaren Mikrozuständen wird bei einem abgeschlossenen System im thermischen Gleichgewicht wahrscheinlicher auftreten als ein Makrozustand mit nur wenigen Mikrozuständen, denn alle Mikrozustände sind im thermischen Gleichgewicht ja gleich wahrscheinlich. Die Zahl die Mikrozustände zu einem Makrozustand ist demnach ein Maß für die Wahrscheinlichkeit des Makrozustandes im thermischen Gleichgewicht. So ist es sehr unwahrscheinlich, dass wir unser System irgendwann wieder im Anfangs-Makrozustand mit nur wenigen Mikrozuständen vorfinden – die Gasteilchen werden kaum freiwillig alle in den rechten Teil des Gasbehälters wandern, auch wenn sie es im Prinzip natürlich könnten. In diesem Sinn ist die Ausbreitung der Gasteilchen im gesamten Gasbehälter irreversibel, also mit extrem hoher Wahrscheinlichkeit unumkehrbar.
Bei einem makroskopisch abgeschlossenen System im thermischen Gleichgewicht ist also die Anzahl \(\Omega\) der Mikrozustände (und damit die Entropie) ein Maß für die Wahrscheinlichkeit des zugehörigen Makrozustandes.
Dabei sind die \(\Omega\)-Zahlen für verschiedene Makrozustände zumeist so extrem groß und zugleich so unterschiedlich, dass ein bestimmter Makrozustand der klaren Favorit ist.
Schauen wir uns als Beispiel dazu wieder den Gasbehälter an. Wie wir unten noch sehen werden, ist die Zahl der Mikrozustände proportional zum Volumen hoch \(N\) (\(N\) = Teilchenzahl, beispielsweise \(10^{20}\)).
Die Zahl der Zustände, bei denen sich die Gasteilchen nur in der rechten Hälfte des Gasbehälters aufhalten, ist also um den Faktor \((1/2)^{N}\) kleiner als die Zahl der Zustände, bei denen sie das ganze Volumen bevölkern können (hätte man auch mit ganz einfacher Wahrscheinlichkeitsrechnung sehen können: die Wahrscheinlichkeit für die rechte Hälfte ist für jedes der \(N\) Teilchen gleich \(1/2\), für alle \(N\) Teilchen also gleich \((1/2)^{N}\)).
Nehmen wir für die Teilchenzahl \(N\) den typischen Wert \(10^{20}\), so ist \( (1/2)^{N} \) eine unglaublich winzige Zahl: Schreibt man sie aus, so kommen hinter dem Komma erst einmal einige Lichjahre nur Nullen. So unwahrscheinlich ist es, dass sich die \(10^{20}\) Gasteilchen alle zugleich für die rechte Hälfte des Gasbehälters entscheiden.
Auch kleinere Abweichungen vom thermischen Gleichgewicht sind sehr unwahrscheinlich. Man kann sich überlegen, dass die statistische Schwankungsbreite zwischen Teilchenanzahl rechts und links im Gleichgewicht etwa bei \(\sqrt{N}\) liegt.
Das bedeutet, dass bei \(10^{20}\) Teilchen die relative Abweichung bei \[ \frac{\sqrt{N}}{N} = \frac{10^{10}}{10^{20}} = 10^{-10} \] liegt. Es ist also bereits sehr unwahrscheinlich, dass der relative Unterschied der Teilchenzahl rechts und links beu deutlich mehr als \(10^{- 8}\) Prozent (also 0,00000001 %) liegt. Zum Vergleich: Eine relative Schwankungsbreite von \( 10^{- 10} \) würde bei einer Länge von einem Kilometer einer Schwankung von nur 0,1 Mikrometer entsprechen – das ist weniger als eine Lichtwellenlänge.
Unser Fazit lautet also: Überlässt man ein makroskopisch abgeschlossenes System sich selbst, so nimmt es schließlich im thermischen Gleichgewicht mit extrem hoher Wahrscheinlichkeit den Makrozustand mit der größten Entropie ein. Das ist der zweite Hauptsatz der Thermodynamik. Fassen wir kurz zusammen:
|
zweite Hauptsatz der Thermodynamik: Überlässt man ein makroskopisch abgeschlossenes System sich selbst, so geht es mit der Zeit ins thermische Gleichgewicht über, d.h. alle erreichbaren Mirkozustände treten mit gleicher Wahrscheinlichkeit auf. Mit extrem hoher Wahrscheinlichkeit befindet sich das System dann im erreichbaren Makrozustand mit der größten Entropie (also mit den weitaus meisten erreichbaren Mikrozuständen).
|
Noch eine Bemerkung zu den anderen Makrozuständen, bei denen sich das System
(noch) nicht im thermischen Gleichgewicht befindet:
Um solche Makrozustände überhaupt angeben zu können, geht man meist
von lokalem thermischen Gleichgewicht aus.
Das bedeutet: schaut man sich nur kleine Teilvolumina an, so befindet sich das System dort bereits in guter Näherung im thermischen Gleichgewicht. Das lässt sich leicht realisieren, denn die Relaxationszeit, die das System braucht, um ins thermische Gleichgewicht zu gelangen, hängt normalerweise stark vom betrachteten Volumen ab. Lokal stellt sich also meist sehr schnell thermisches Gleichgewicht ein. Nur so kann man statistische Zustandsgrößen wie Temperatur, Druck oder Dichte auch lokal definieren. Der Makrozustand ist dann durch die großräumige Verteilung dieser Größen definiert, beispielsweise durch eine Dichteverteilung. Das obiger Beispiel mit dem Gasbehälter, bei dem sich anfangs alle Gasteilchen in der rechten Hälfte befinden, hat das sehr schön gezeigt, denn er ist (u.a.) durch eine Dichteverteilung charakterisiert: Rechts ist die Dichte konstant positiv, links ist sie Null.
Wir hatten einen Makrozustand oben als statistische Zusammenfassung sehr vieler Mikrozustände definiert. Dabei müssen wir nun festlegen, welche Mikrozustände wir mit welcher Wahrscheinlichkeit zu einem Makrozustand zusammenfassen wollen. Diese Zusammenfassung von Mikrozuständen zu einem Makrozustand bezeichnet man auch als statistisches Ensemble, statistische Verteilung oder auch als statistische Gesamtheit des Makrozustandes – ich werde hier alle drei Begriffe synonym verwenden. Beispielsweise war oben der Anfangs-Makrozustand bei dem Gasbehälter durch alle Mikrozustände charakterisiert, bei denen sich die Gasteilchen in der rechten Hälfte befinden.
Wir wollen uns nun den Prototyp einer statistischen Gesamtheit ansehen: das sogenannte mikrokanonische Ensemble. Die gesamte Physik des thermischen Gleichgewichtes lässt sich aus diesem Ensemble ableiten.
Um welchen Makrozustand geht es dabei? Wir betrachten ein makroskopisch abgeschlossenes System im thermischen Gleichgewicht mit einer bestimmten Teilchenzahl \(N\) (nur eine Teilchensorte), das ein bestimmtes Volumen \(V\) einnimmt und dessen Gesamtenergie sich ein einem sehr kleinen Energieintervall zwischen den Werten \(E\) und \( E + \delta E \) befindet – diese drei Angaben definieren unseren Makrozustand.
Bei Gasen im thermischen Gleichgewicht ist das aureichend. Bei Festkörpern können noch andere Größen wie Magnetisierung oder innere Spannung wichtig sein, aber das wollen wir hier nicht betrachten. Ist das System noch nicht im thermischen Gleichgewicht, so sind weitere makroskopische Größen notwendig, um den Makrozustand zu kennzeichnen, beispielsweise eine ortsabhängige Energie- oder Dichteverteilung (wobei man dann lokales thermisches Gleichgewicht annimmt – wir hatten es oben bereits kurz angesprochen).
Was bedeutet nun der Begriff klein für das Energieintervall \( \delta E \)?
Er besagt, dass \(\delta E\) sehr viel kleiner als die Gesamtenergie \(E\) sein soll. Allerdings soll \(\delta E\) dabei immer sehr viel größer bleiben als der typische Energieabstand zwischen benachbarten Mikrozuständen, so dass noch sehr viele Mikrozustände im Energieintervall liegen.
Die Energieintervallbreite \(\delta E\) soll also aus makroskopischer Sicht klein, aber aus mikroskopischer Sicht groß sein – wir werden das unten noch präzisieren.
Da der Energieabstand zwischen den Mikrozuständen exponentiell mit der Teilchenzahl \(N\) abnimmt, ist das kein Problem: auch sehr kleine Werte für \(\delta E\) (im Vergleich zu \(E\)) sind immer noch weit größer als der Energieabstand der Mikrozustände.
Übrigens kann man \(\delta E\) auch als die quantenmechanische Unschärfe der Energiemessung interpretieren, die bei einer endlichen Messzeit prinzipiell auftritt. Demnach tragen zum Messergebnis alle Mikrozustände bei, die in dieser Energieunschärfe liegen. Bei einer Messzeit von einer Millisekunde hätte man beispielsweise eine Energieunschärfe von ungefähr \( \delta E = 10^{- 12} \mathrm{eV} \), während die Gesamtenergie \(E\) eines makroskopischen Körpers normalerweise weit über \(1 \mathrm{eV}\) liegt.
Einige Anmerkungen dazu:
Man kann manchmal auch ohne das Energieintervall \( \delta E \) auskommen, und zwar dann, wenn nur hochgradig entartete Mikrozustände auftreten, also sehr viele Mikrozustände mit derselben Energie \(E_{n}\), wobei die einzelnen \(E_{n}\) relativ große Abstände haben, vergleichbar mit den Abständen der Einteilchen-Energieniveaus.
Das geschieht beispielsweise, wenn die Einteilchenniveaus konstante Abstände haben (Beispiel harmonischer Oszillator) oder es nur zwei Einteilchenniveaus gibt (Beispiel Spinsystem, siehe unten).
Bei einem hochgradig entarteten Mikrozustand mit Energie \(E_{n}\) ist die Situation gleichsam so, als hätte man oben im Energieintervall von \( E \) bis \( E + \delta E \) alle darin liegenden Mikrozuständen energetisch zu einem Energieniveau \(E = E_{n}\) zusammengeschoben. Statt des Energieintervalls kann man dann direkt die Energie \(E_{n}\) zur Charakterisierung des Makrozustandes verwenden, denn dieser umfasst dann ja bereits sehr viele Mikrozustände.
Letztlich ist es für die Makrozustände egal, ob man ein Energieniveau \(E_{n}\) betrachtet, das sehr viele Mikrozustände gleicher Energie umfasst, oder ob man ein sehr schmales Energieintervall von \( E \) bis \( E + \delta E \) betrachtet, in dem vergleichbar viele Mikrozustände energetisch eng benachbart liegen.
Baut man die statistische Physik alleine auf der klassischen Mechanik auf, so ist \( \Omega(E) \) proportional zum Volumen des Phasenraums, den das System bei Energie zwischen \(E\) und \(E + \delta E\) einnimmt (der Phasenraum wird dabei durch die Orts- und Impulswerte der \(N\) Teilchen aufgespannt – er ist also 6N-dimensional). Der dabei notwendige Proportionalitätsfaktor ist im Prinzip willkürlich, so dass die Entropie nur bis auf eine beliebige additive Konstante festgelegt ist – wir hatten es oben bereits erwähnt.
Statt Energie wird in der Thermodynamik auch oft der Begriff innere Energie verwendet und mit \(U\) statt \(E\) abgekürzt. Damit möchte man klarmachen, dass beispielsweise keine Energien gemeint sind, die auf einer makroskopischen Bewegung des Systems beruhen.
Wir hatten gesagt, dass das System makroskopisch abgeschlossen oder auch makroskopisch isoliert sein soll. Was damit gemeint ist, wissen wir jetzt: \(E, V\) und \(N\) sollen fest vorgegeben sein, wobei allerdings minimale Energieschwankungen innerhalb des kleinen Energieintervalls \(\delta E\) erlaubt sein sollen, denn man kann ein makroskopisches System nie vollständig isolieren.
Deshalb haben wir keine absolut scharfe Energie \(E\) vorgegeben, sondern ein sehr kleines Energieintervall. Die Energie darf diesen kleinen Bereich nicht verlassen – das bedeutet makroskopisch abgeschlossen.
Später müssen wir dann untersuchen, welchen Einfluss die Energie-Schwankungsbreite \(\delta E\) auf unsere Ergebnisse hat. Wir werden sehen: Die Zahl der Zustände im Energieintervall ist proportional zur Intervallbreite \(\delta E\) (ist ja klar), aber der Logarithmus dieser sehr großen Zahl (und damit die Entropie) ist fast unabhängig von \(\delta E\), solange es makroskopisch klein und mikroskopisch groß ist – Details dazu weiter unten.
Noch eine Anmerkung:
Später werden wir beim kanonischen Ensemble noch sehen, was geschieht, wenn wir die Forderung nach einem bestimmten Energieintervall aufgeben und stattdessen nur noch eine mittlere Energie (oder gleichwertig dazu eine Temperatur) vorgeben. Ein solches System muss dann nicht mehr makroskopisch abgeschlossen sein, so dass man seine Energiefluktuationen dann realistischer beschreiben kann. Für makroskopische Systeme zeigt sich dabei, dass größere Energiefluktuationen extrem unwahrscheinlich sind. Auch ein solches System kann man daher makroskopisch sehr gut durch das mikrokanonische Ensemble mit seinem strengen Energieintervall beschreiben. Kanonisches und mikrokanonisches Ensemble sind für die thermodynamischen Eigenschaften makroskopischer Systeme gleichwertig – mehr dazu später.
Welche quantenmechanischen Zustände eignen sich als Mikrozustände? Naheliegend wäre es nach den obigen Überlegungen, die Energieeigenzustände des Systems zu verwenden, denn die Energie wird ja vorgegeben, also (mit einer gewissen Unschärfe) gemessen.
Im Prinzip wäre es auch denkbar, andere Quantenzustände als Mikrozustände zu nehmen, die aus einer Superposition von Energieeigenzuständen bestehen. Das würde dann Sinn machen, wenn wir Zusatzinformationen gemessen hätten, die eine solche Superposition festlegen. Das tun wir aber hier nicht – wir messen lediglich die Gesamtenergie und stellen fest, dass sie zwischen \( E \) und \( E + \delta E \) liegt. Außerdem müsste eine solche Superposition stabil gegen kleine äußere Einflüsse sein, was meist nicht der Fall ist (siehe Anhang unten).
Wenn sich der Mikrozustand des Systems ändert, so geschieht das aufgrund der geringen Wechselwirkung mit der Umgebung – es könnten beispielsweise energiearme Photonen ausgesendet oder eingefangen werden (Wärmestrahlung). Die Umgebung merkt also im Prinzip etwas davon, dass sich der Mikrozustand ändert, und wir könnten durch eine präzise Messung des Gesamtsystems aus unserem beobachteten System und seiner Umgebung theoretisch herausfinden, wie sich der Mikrozustand des Systems geändert hat.
Eine solche Messung, die die Umgebung einbezieht (und damit letztlich das gesamte Universum), ist jedoch für lokal existierende Wesen wie uns absolut unmöglich. Wir messen nur, dass sich die Gesamtenergie unseres lokalen makroskopischen Objekts mit der Unschärfe \(\delta E\) bei \(E\) befindet.
Aus Die Symmetrie der Naturgesetze, Kapitel 4.2 wissen wir, dass wir dann klassisch über alle Mikrozustände mitteln müssen, deren Energie in dem vorgegebenem Intervall liegen. Das genau meinen wir, wenn wir sagen, die Gesamtenergie des Systems liegt in dem Energieintervall. In Anhang 2 unten können Sie im Detail nachlesen, wie eine solche klassische Mittelung entsteht, wenn man über die vielen nicht beobachteten Mikrozustände der Umgebung summiert.
Als Mikrozustände unseres Systems verwenden wir also die Energieeigenzustände \( |n\rangle \) mit Energie \(E_{n}\), wobei alle die Mikrozustände erreichbar sind, deren Energie zwischen \( E \) und \( E + \delta E \) liegt. Die Wahrscheinlichkeit, mit der der Energiezustand \( |n\rangle \) zu einer Messung beiträgt, nennen wir \(P_{n}\).
Im Prinzip sind zunächst einmal alle möglichen Wahrscheinlichkeiten \( P_{n} \) denkbar, sogar mit Zeitabhängigkeit. Sie entsprechen Systemen, die sich nicht im thermischen Gleichgewicht befinden. Das kann sehr kompliziert werden. Wir wollten uns aber hier den einfachen Fall anzusehen: ein makroskopisch isoliertes System im thermischen Gleichgewicht.
Oben haben wir gesehen, dass dann alle Wahrscheinlichkeiten \(P_{n}\) zeitunabhängig und gleich groß werden – das geht übrigens nur, wenn die Mikrozustände zugleich Energieeigenzustände sind, denn Superpositionen von Energieeigenzuständen ergeben immer eine Zeitabhängigkeit.
Bezeichnen wir die Zahl der Mikrozustände mit Energie zwischen \(E\) und \( E + \delta E \) mit \( \Omega(E) \), so ist \[ P_{n} = \frac{1}{\Omega(E)} \] für Mikrozustände \( |n\rangle \) mit Energie \(E_{n}\) zwischen \(E\) und \(E + \delta E\). Für Mikrozustände außerhalb dieses Energieintervalls ist dagegen \( P_{n} = 0 \).
Zur Erinnerung:
Ddie Intervallbreite \(\delta E\) soll zwar sehr viel kleiner als \(E\) sein, aber der Abstand
energetisch benachbarter Mikrozustände soll zugleich sehr viel kleiner als \(\delta E\) sein, so dass
auch in einem makroskopisch schmalen Energieintervall noch extrem viele Mikrozustände liegen.
Die Zahl der Zustände \(\Omega(E)\) im Energieintervall ist also eine sehr große Zahl.
Man kann sich vorstellen, dass die Energien der Mikrozustände extrem dicht beieinanderliegen, so dass man gleichsam ein energetisches Quasi-Kontinuum von Mikrozuständen vor sich hat. Dieses Quasi-Kontinuum besitzt eine Zustandsdichte \( \omega(E) \) im Energieintervall, wobei die Intervallbreite \( \delta E \) so klein sein soll, dass sich diese Zustandsdichte innerhalb des Intervalls kaum ändert. Es soll also in sehr guter Näherung \[ \Omega(E) = \omega(E) \cdot \delta E \] gelten. Die Zustandsdichte \(\omega(E)\) behandeln wir in sehr guter Näherung als stetige Funktion der Energie.
Wem das merkwürdig vorkommt: Der gewohnte Begriff der Dichte (Masse pro Volumen) ist ganz ähnlich zu verstehen: Auch bei der Dichte betrachtet man kleine Volumina \(\delta V\), die groß genug sind, um sehr viele Teilchen zu enthalten, die aber zugleich klein sind im Vergleich zum betrachteten Gesamtvolumen. Bei 3 Teilchen in einem Volumen macht der Begriff Dichte für Teilvolumina dann natürlich keinen Sinn mehr.
Insgesamt haben wir also:
|
mikrokanonisches Ensemble: Wir betrachten ein makroskopisches abgeschlossenes System im thermischen Gleichgewicht mit einer bestimmten Teilchenzahl \(N\), einem bestimmten Volumen \(V\) und einer Gesamtenergie im schmalen Energieintervall zwischen \( E \) und \( E + \delta E \). Dabei ist \( \delta E \) sehr viel kleiner als die Gesamtenergie \(E\), aber sehr viel größer als die winzigen Energieabstände benachbarter Mikrozustände. Die Wahrscheinlichkeit für einen Mikrozustand mit Energie \(E_{n}\) ist dann im Energieintervall unabhängig von \(n\): \[ P_{n} = \frac{1}{\Omega(E)} = \frac{1}{\omega(E) \cdot \delta E} \] für \(E_{n}\) zwischen \(E\) und \(E + \delta E\) und \( P_{n} = 0 \) außerhalb dieses Energieintervalls. Dabei ist \(\Omega(E)\) die Zahl der Mikrozustände im schmalen Energieintervall und \(\omega(E)\) ist die mittlere Zustandsdichte im Intervall.
|
Versuchen wir, \(\Omega(E)\) und anschließend \( \ln{\Omega(E)} \) (und damit letztlich die Entropie des Makrozustandes) grob abzuschätzen und so die Zahlen nachzuvollziehen, die wir oben bereits erwähnt hatten (die Rechnung findet man beispielsweise im Berkeley Physik Kurs, Band 5: Statistische Physik, Kapitel 3.5).
Schauen wir uns dazu ein ideales Gas in einem Würfel mit Kantenlänge \(L\) an. In einem ersten Schritt wollen wir herausfinden, wieviele Energieniveaus \(\phi(E)\) es unterhalb einer maximalen Gesamtenergie \(E\) gibt.
Dazu nehmen wir vereinfacht an, dass dann auch jedes der \(N\) Gasteilchen maximal einen Energiebetrag \[ \epsilon := \frac{E}{N} \] zur Verfügung hat.
Bei Zimmertemperatur ist \(\epsilon\) typischerweise 1/40 eV.
Wie viele quantenmechanischen Energieniveaus kann ein einzelnes Gasatom mit einer Energie unterhalb von \(\epsilon\) in dem Kasten erreichen? Machen wir es uns einfach und betrachten wir nur Schwingungen der Quanten-Teilchenwelle in einer Dimension. In diese Dimension der Länge \(L\) passen dann \(n\) Wellenberge hinein, wobei die Energie der entsprechenden stehenden Teilchenwelle mit \(n^{2}\) anwächst (siehe Wikipedia: Teilchen im Kasten; die Rechnung basiert auf der nichtrelativistischen Quantenmechanik). Das höchste erreichbare \(n\) ist dann: \begin{align} n &= \frac{L}{ \pi \hbar} \, \sqrt{2 M \epsilon} = \\ &= \frac{L}{ \pi \hbar c} \, \sqrt{2 M c^{2} \epsilon} \end{align} mit \( \hbar = \frac{h}{2\pi} \) und der Teilchenmasse \(M\).
Versuchen wir daraus eine besser handhabbare Formel zu machen, in die wir \(L\) in Metern, \(M c^{2}\) in GeV und \(\epsilon\) in eV direkt einsetzen können. Dazu verwenden wir den bekannten Wert \[ \hbar c = 200 \, \mathrm{MeV} \, \mathrm{fm} = \] \[ = 200 \cdot 10^{6} \, \mathrm{eV} \cdot 10^{-15} \, \mathrm{m} = \] \[ = 2 \cdot 10^{-7} \, \mathrm{m} \cdot \mathrm{eV} = \] \[ = 2 \cdot 10^{-7} \, \mathrm{m} \cdot \sqrt{ 10^{- 9} \, \mathrm{GeV} \cdot \mathrm{eV}} = \] \[ = 6,3 \cdot 10^{-12} \, \mathrm{m} \cdot \sqrt{\mathrm{GeV} \cdot \mathrm{eV}} \] Entsprechend ist \[ \frac{1}{\pi \hbar c} \, \sqrt{2} = 7 \cdot 10^{10} \frac{1}{\mathrm{m} \cdot \sqrt{\mathrm{GeV} \cdot \mathrm{eV}}} \] Also ist \[ n = 7 \cdot 10^{10} \, L[\mathrm{m}] \, \sqrt{M[\mathrm{GeV}] \cdot \epsilon[\mathrm{eV}]} \] Setzen wir also für die Kastenlänge \(L\) einen Meter ein, für \(M\) die Masse eines Wasserstoffatoms (also 1 GeV) und für \(\epsilon\) den obigen Wert von 1/40 eV (entspricht etwa Zimmertemperatur), so haben wir ungefähr \[ n = 10^{10} \] also etwa 10 Milliarden Wellenberge.
Lässt man auch Schwingungen in den anderen beiden Raumdimensionen zu, so muss man dieses Ergebnis im Wesentlichen hoch 3 nehmen, was die Zahl \(n\) auf etwa \(10^{30}\) erhöht.
Die Zahl der Einteilchen-Energieniveaus, die ein Teilchen mit einer Teilchenenergie kleiner-gleich \(\epsilon\) alle erreichen kann, wollen wir konkret mit \(\varphi(\epsilon)\) bezeichnen. In drei Raumdimensionen würde unser obiges Beispiel grob folgenden Schätzwert liefern (auf Vorfaktoren soll es hier nicht ankommen – es geht um einen groben Schätzwert für die Größenordnung): \[ \varphi(\epsilon) = 10^{30} \, (L[\mathrm{m}])^{3} \, ( M[\mathrm{GeV}] \cdot \epsilon[\mathrm{eV}] )^{3/2} \] Ein einzelnes Wasserstoffatom hat bei Zimmertemperatur in einem Kubikmeter Volumen also etwa \(10^{30}\) Quantenzustände zur Verfügung.
Auch andere Teilchen in makroskopische Systemen werden sich ähnlich verhalten, d.h. wir gehen generell von der folgenden Annahme aus (wobei wir die unwichtige Abhängigkeit von der Teilchenmasse \(M\) in den Vorfaktor integrieren):
|
Anzahl der Einteilchenzustände bis zu einer Einteilchenenergie \(\epsilon\): Die Zahl der Einteilchenzustände \(\varphi(\epsilon)\), die ein einzelnes Teilchen mit einer Teilchenenergie kleiner-gleich \(\epsilon\) in einem typischen makroskopischen System mit Volumen \(V\) erreichen kann, kann man durch folgende Formel grob abschätzen: \[ \varphi(\epsilon) = B \, V \, \epsilon^{b} \] Der Exponent \(b\) ist von der Größenordnung 1 (beispielsweise 3/2). Wird das Volumen \(V\) in einer makroskopischen Einheit gemessen (z.B. Kubikmeter) und die maximale Teilchenenergie \(\epsilon\) in einer mikroskopischen Einheit gemessen (z.B. eV), so ist \(B\) eine große Zahl (beispielsweise \(10^{30}\)).
|
Wieviele N-Teilchen-Zustände (also nicht mehr nur Einteilchenzustände wie bisher)
sind dann in diesem makroskopischen System
unterhalb einer Gesamtenergie von
\[
E = N \, \epsilon
\]
möglich?
Um das auszurechnen, machen wir eine Vereinfachung:
Den N-Teilchen-Mikrozustand bilden wir einfach, indem wir die N-Teilchen alle irgendwie zufällig auf die Einteilchenzustände verteilen.
Wir interessieren uns also nicht für Wechselwirkungen zwischen den Teilchen, und wir lassen Aspekte wie die (Anti-) Symmetrie der Wellenfunktion bei identischen Teilchen außer acht. Anders ausgedrückt: Wir betrachten ein ideales Gas aus unterscheidbaren Teilchen.
Haben unsere Teilchen beispielsweise Spin 1/2, so wollen wir das Pauli-Prinzip vernachlässigen, d.h. ein Einteilchenniveau darf auch von mehreren Teilchen besetzt sein. Das ist ok, solange wesentlich mehr Einteilchenzustände als Teilchen zur Verfügung stehen, d.h. solange \(\varphi(\epsilon)\) sehr viel größer als \(N\) ist.
Wenn beispielsweise \(10^{20}\) Teilchen auf \(10^{30}\) Einteilchenniveaus verteilt werden sollen, so kommt es nur selten vor, dass Einteilchenniveaus mehrfach besetzt werden müssen. Das ist für typische Gasen bei Atmosphärendruck und Zimmertemperatur der Fall, nicht aber beispielsweise bei der stark komprimierten Sternmaterie eines weißen Zwerges oder eines Neutronensterns – mehr dazu weiter unten beim Thema ideale Quantengase.
Wie viele Möglichkeiten gibt es nun, die \(N\) Teilchen auf die \(\varphi(\epsilon)\) Einteilchenzustände zu verteilen, wenn wir Mehrfachbesetzung zulassen?
Das erste Teilchen hat \(\varphi(\epsilon)\) Möglichkeiten, das zweite Teilchen ebenfalls usw., d.h. die Gesamtzahl der N-Teilchen-Zustände unterhalb einer Gesamtenergie \(E\) ist ungefähr gleich \[ [\varphi(\epsilon)]^{N} \] Dabei haben wir noch eine weitere Vereinfachung vorgenommen: Wir haben die Möglichkeiten weggelassen, bei denen einige Teilchen eine Energie oberhalb von \(\epsilon = E/N\) haben, was durch andere energiearme Teilchen ja wieder ausgeglichen werden könnte. All das spielt letztlich keine Rolle, da es uns später nicht um die genaue Zustandsanzahl geht, sondern nur um ihren Logarithmus – der merkt von solchen Feinheiten überhaupt nichts. Halten wir fest:
|
Anzahl der N-Teilchen-Zustände bis zu einer Gesamtenergie \(E\):
Die Gesamtzahl \(\phi(E)\) der N-Teilchen-Zustände (Mikrozustände) unterhalb einer Gesamtenergie \( E = N \, \epsilon \) in einem typischen makroskopischen System mit Volumen \(V\) kann man durch folgende Formel grob abschätzen: \[ \phi(E) = [\varphi(\epsilon)]^{N} = B^{N} V^{N} \epsilon^{b \, N} \] mit \(\epsilon = E/N\). Für \(b, B, V\) und \(\epsilon\) gilt das bei \(\varphi(\epsilon)\) gesagte (siehe das Kästchen weiter oben).
|
Die Formel gilt beispielsweise für ein ideales Gas bei Zimmertemperatur.
Obwohl die Formel harmlos aussieht, hat sie es in sich, denn die Zahl der Zustände
wächst wegen der Teilchenzahl \(N\) im Exponenten
extrem rasch mit der maximalen Gesamtenergie oder dem verfügbaren Volumen an.
Hier sehen wir auch die Proportionalität mit \(V^{N}\), die wir oben
in unserem Gasbehälter-Beispiel bereits verwendet haben. \(\Omega(E)\) hat dieselbe
Volumen-Abhängigkeit wie \(\phi(E)\) (sieht man anhand der Formel
\( \Omega(E) = \frac{d \phi}{d E} \, \delta E \), die gleich kommt).
Mit der Anzahl \(\phi(E)\) der Zustände bis zur Energie \(E\) können wir nun leicht die Anzahl \(\Omega(E)\) der Zustände im Energieintervall zwischen \(E\) und \(E + \delta E\) ausrechnen, wobei wir ausnutzen, dass \(\delta E\) sehr viel kleiner als \(E\) ist: \[ \Omega(E) = \phi(E + \delta E) - \phi(E) = \] \[ = \frac{d \phi}{d E} \, \delta E = \] \[ = \frac{d \phi}{d \epsilon} \, \frac{d \epsilon}{d E} \, \delta E = \] \[ = \frac{d [\varphi(\epsilon)]^{N}}{d \epsilon} \, \frac{d \epsilon}{d E} \, \delta E = \] \[ = N \, [\varphi(\epsilon)]^{N - 1} \, \frac{d\varphi(\epsilon)}{d \epsilon} \, \frac{1}{N} \, \delta E = \] \[ = [\varphi(\epsilon)]^{N - 1} \, \frac{d\varphi(\epsilon)}{d \epsilon} \, \delta E \] Nun bilden wir den Logarithmus dieser Zahl, d.h. wir interessieren uns für die Zahl der Stellen, die man zum Aufschreiben von \(\Omega(E)\) ungefähr braucht: \[ \ln{\Omega(E)} = \] \[ = \ln{ \left( [\varphi(\epsilon)]^{N - 1} \, \frac{d\varphi(\epsilon)}{d \epsilon} \, \delta E \right)} = \] \[ = (N - 1) \, \ln{\varphi(\epsilon)} + \ln{ \left( \frac{d\varphi(\epsilon)}{d \epsilon} \, \delta E \right)} \] Wir wollen nun sicherstellen, dass der zweite Term gegenüber dem ersten Term vernachlässigbar ist – das ist der Fall, wenn \(\delta E\) sich in einem Bereich befindet, in dem \[ \frac{d\varphi(\epsilon)}{d \epsilon} \, \delta E = \] \[ = \frac{d [B \, V \, \epsilon^{b}]}{d \epsilon} \, \delta E = \] \[ = B \, V \, b \, \epsilon^{b - 1} \, \delta E \] größer als 1 und zugleich klein genug ist (also nicht mit einer Zahl hoch \(N\) anwächst). Da \(b\) ungefähr gleich 1 ist, ist der Term von der Größenordnung \( B \, V \, \delta E \). Die entscheidende Bedingung an \(\delta E\), die dessen unteres Limit (mikroskopisch groß) festlegt, lautet also:
Misst man die Energien in eV und das Volumen V in Kubikmetern, so ist \(B\) beispielsweise von der Größenordnung \(10^{30}\) und \(V\) ist von der Größenordnung Eins. Das Energieintervall \(\delta E\) muss also mindestens \(10^{- 30}\) eV betragen – das sind etwa die Energieabstände für die Ein-Teilchen-Zustände im Volumen \(V\), wie wir oben gesehen haben. Klar: \( \frac{d\varphi(\epsilon)}{d \epsilon} \, \delta E \) ist ja ungefähr die Anzahl der Ein-Teilchen-Zustände im Energieintervall \(\delta E\). Damit sind zu kleine Argumente im zweiten Logarithmus-Term schon mal vom Tisch.
Zugleich soll \(\delta E\) makroskopisch klein sein, also sehr viel kleiner als \(E\). Da \(E = N \, \epsilon \) ist, sind wir auf der sicheren Seite, wenn wir für \(\delta E\) maximal die typischen Ein-Teilchen-Energien \(\epsilon\) von bis zu einigen eV zulassen. Dann ist nämlich \(B \, V \, \delta E \) etwa von der Größenordnung \(10^{30}\), so dass der Logarithmus dieses zweiten Terms für makroskopische Teilchenzahlen \(N\) wieder vollkommen vernachlässigbar gegenüber dem ersten Logarithmus-Term ist, der mit \(N\) anwächst.
|
Größe des Energieintervalls \(\delta E\):
|
Zum Vergleich:
Wenn wir \(\delta E\) als die quantenmechanische Energieunschärfe bei endlicher Messzeit
interpretieren, so hatten wir oben bei
einer Messzeit von einer Millisekunde eine Energieunschärfe
von ungefähr \( \delta E = 10^{- 12} \mathrm{eV} \) erhalten.
Das passt wunderbar in den geforderten Bereich.
Mit der obigen Forderung an \(\delta E\) haben wir sichergestellt, dass der zweite Logarithmus-Term vernachlässigbar gegenüber dem ersten Logarithmus-Term wird, so dass wir in sehr guter Näherung schreiben können: \[ \ln{\Omega(E)} = (N - 1) \, \ln{\varphi(\epsilon)} \] Da \(\varphi(\epsilon)\) von der Größenordnung \(10^{30}\) ist, liegt \( \ln{\varphi(\epsilon)} \) irgendwo unter 100 . Die 1 spielt gegenüber \(N\) praktisch keine Rolle, so dass wir auch \[ \ln{\Omega(E)} = N \, \ln{\varphi(\epsilon)} = \] \[ = \ln{ \left( [\varphi(\epsilon)]^{N} \right)} = \ln{\phi(E)} \] schreiben können. Wir können also sagen:
|
Der Logarithmus der Zustandszahl: \(\ln{\Omega(E)}\) ist von der Größenordnung der Teilchenanzahl \(N\) des Systems. In sehr guter Näherung gilt: \[ \ln{\Omega(E)} = N \, \ln{\varphi(\epsilon)} = \] \[ = \ln{ \left( [\varphi(\epsilon)]^{N} \right)} = \ln{\phi(E)} \] Dabei ist \( \Omega(E) \) die Zahl der Mikrozustände im Energieintervall zwischen \(E\) und \(E + \delta E\), \(\phi(E)\) ist die Gesamtzahl der Mikrozustände unterhalb der Gesamtenergie \(E\) und \(\varphi(\epsilon)\) ist die Zahl der Einteilchen-Zustände unterhalb der Teilchenenergie \(\epsilon = E/N\) im Volumen des makroskopischen Systems. Dabei spielt die Breite des Energieintervalls \(\delta E\) für \( \ln{\Omega(E)} \) und damit für die Entropie praktisch keine Rolle, solange \(\delta E\) im oben genannten Bereich liegt (makroskopisch klein, mikroskopisch groß). |
Für den Logarithmus der Zustandszahl spielt es also praktisch keine Rolle,
ob wir nur die Zahl der Zustände im kleinen Energieintervall \(\delta E\)
bei \(E\) nehmen oder die Gesamtzahl aller Zustände
bis zur Energie \(E\) betrachten, sofern die
Breite des Energieintervalls \(\delta E\) die obige Bedingung erfüllt
(also makroskopisch klein und zugleich mikroskopisch groß ist).
Das bedeutet, dass die Anzahl Dezimalstellen dieser beiden extrem großen Zahlen \( \Omega(E) \) und \(\phi(E)\) etwa von derselben Größe ist, nämlich von der Größenordnung der Teilchenanzahl \(N\) im System.
Oben hatten wir gesehen, dass man durchaus Lichtjahre an Platz braucht, um solche Zahlen auszuschreiben. Da spielt es für die Anzahl Stellen keine Rolle, ob man 10 Stellen mehr oder weniger hinschreiben muss. Die Zahlen selber würden sich dabei sehr wohl um einen Faktor \(10^{10}\) unterscheiden, sind also keineswegs gleich groß. Sie haben nur fast dieselbe Stellenanzahl und damit ziemlich genau denselben Logarithmus.
Das ist auch der Grund dafür, warum \( \delta E \) keine Rolle spielt, solange es zwischen sagen wir \(10^{- 30}\) eV und 1 eV liegt. Variiert man \(\delta E\) in diesem Bereich, so verändert man die Zahl der Zustände \(\Omega(E)\) in diesem Intervall um einen Faktor bis zu \(10^{30}\). Die Zahl der Stellen verändert sich also um bis zu 30 Stellen, was bei \(10^{20}\) Stellen ziemlich egal ist – der Logarithmus merkt davon also praktisch nichts.
Die Zustandszahl \(\Omega(E)\) merkt die Änderung sehr wohl. Daher ist auch der oft verwendete Satz, dass fast alle Zustände bis zur Energie \(E\) ganz oben zwischen \(E\) und \(E + \delta E\) liegen, etwas irreführend, denn \(\phi(E)\) kann sehr wohl deutlich größer als \(\Omega(E)\) sein. Was praktisch gleich groß ist, ist die Stellenanzahl beider Zahlen und damit ihr Logarithmus.
Andererseits stimmt der Satz auch: Da \(\phi(E)\) ungefähr mit \(E^N\) anwächst und die Teilchenzahl \(N\) ja eine sehr große Zahl ist, liegen die meisten Zustände tatsächlich im Bereich sehr nahe bei \(E\). Die Zustände werden mit wachsender Energie sehr schnell immer dichter.
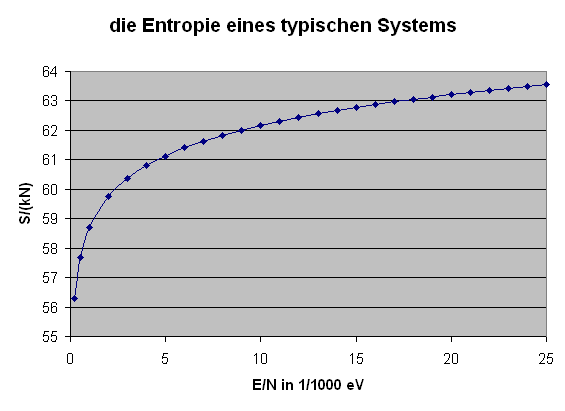
Die obige Formel ermöglicht es uns nun, die Entropie eines typischen Systems (beispielsweise eines idealen Gases) als Funktion der Energie darzustellen: \[ S = k \, \ln{\Omega(E)} = \] \[ = k \, N \, \ln{\varphi(\epsilon)} = \] \[ = k \, N \, \ln{\left(B \, V \, \epsilon^{b} \right)} \] Hier setzen wir für \(V\) einen Kubikmeter ein, messen \(\epsilon\) in eV und verwenden \(b = 3/2\), so dass \(B = 10^{30}\) ein vernünftiger Wert ist. Damit erhalten wir \[ \frac{S}{k \, N} = \ln{\left(10^{30} \, \epsilon^{3/2} \right)} \] mit \(\epsilon\) in eV. Die folgende Grafik stellt \( \frac{S}{k \, N} \) bis zu \( \epsilon = 1/40 \, \mathrm{eV} \) dar, was der typischen Teilchenenergie bei Zimmertemperatur entspricht:
Die wesentliche Eigenschaft der Temperatur ist es, dass zwei Körper, die Wärme austauschen können, schließlich ihre Temperatur aneinander angleichen – man spricht auch vom nullten Hauptsatz der Thermodynamik. Wärmeaustausch bedeutet Energieaustausch, ohne dass sich die äußeren Parameter der Körper (insbesondere das Volumen oder bei Festkörpern beispielsweise die Scherung oder die Magnetisierung) ändern. Auch ein Austausch von Teilchen soll ausgeschlossen sein. Ab sofort werden wir als Beispiel für äußere Parameter immer das Volumen nehmen, was natürlich besonders bei Gasen sinnvoll ist – andere äußere Parameter werden analog behandelt. Ein äußerer Parameter ist dabei generell ein Parameter, der die Energieniveaus der Mikrozustände ändert, nicht aber ihre Wahrscheinlichkeiten. Anders ausgedrückt: der Hamiltonoperator des Systems bzw. die Randbedingungen hängen von dem äußeren Parameter ab.
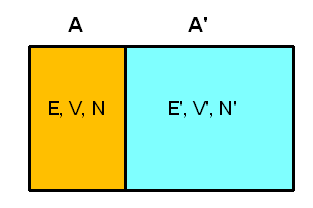
Versuchen wir, eine Größe mit den Eigenschaften einer Temperatur auf Basis unseres mikrokanonischen Ensembles statistisch zu definieren. Dazu betrachten wir zwei isolierte makroskopische Systeme A und A', die jeweils \(N\) bzw. \(N'\) Teilchen beinhalten, ein Volumen \(V\) bzw. \(V'\) ausfüllen und eine Energie zwischen \(E\) und \(E + \delta E\) bzw. zwischen \(E\)' und \(E' + \delta E'\) aufweisen.
Wir können uns beispielsweise zwei Gasbehälter mit guter Isolierung vorstellen. Jedes System soll für sich im thermischen Gleichgewicht sein, d.h. sein Makrozustand kann durch unser mikrokanonisches Ensemble oben beschrieben werden und ist durch die Zustandsgrößen \((N, V, E)\) bzw. \((N', V', E')\) gekennzeichnet (die kleinen Energieintervalle lassen wir weg, da sie für den Logarithmus und damit für den Makrozustand ja uninteressant sind, wie wir bereits wissen).
Nun wollen wir eine thermische Verbindung zwischen den Systemen schaffen. Beispielsweise könnten die beiden Gasbehälter eine feststehende gemeinsame Wand aus wärmeleitendem Metall aufweisen. Volumen und Teilchenzahl der beiden Systeme können sich dabei nicht ändern, d.h. die Energieniveaus der Mikrozustände bleiben unverändert. Aber: Die Möglichkeit, Energie zwischen den Systemen auszutauschen, macht neue Mikrozustände für das zusammengesetzte Gesamtsystems zugänglich, die vorher verboten waren! Was sich deshalb ändert, sind die Wahrscheinlichkeiten \(P_{n}\) und \(P_{n}'\), mit denen die Energieniveaus besetzt sein können.
Man bezeichnet die Energiemenge, die ein System absorbiert, ohne dass dies auf eine
geänderte Teilchenzahl oder ein geändertes Volumen zurückgeführt werden kann,
als Wärmemenge \(Q\).
|
Die Wärmemenge \(Q\): Absorbiert ein makroskopisches System eine makroskopische Energiemenge \(\Delta E\), ohne dass dies auf geänderte äußere Parameter (Volumen) und damit geänderte Energieniveaus der Mikrozustände oder eine Änderung der Teilchenzahl zurückgeführt werden kann, so bezeichnet man diese Energiemenge als Wärmemenge \(Q\). |
Zur Vereinfachung wollen wir davon ausgehen, dass der Energiefluss langsam abläuft,
so dass sich jedes der beiden Teilsysteme A und A' einzeln ständig annähernd
im thermischen Gleichgewicht befindet. Man spricht dann von einem quasi-statischen Prozess.
Deshalb können wir während des Energieflusses jedes Teilsystem für sich
recht gut durch ein mikrokanonisches Ensemble
beschreiben, d.h. die jeweils erreichbaren Mikrozustände
zwischen \(E\) und \(E + \delta E\) bzw. zwischen \(E'\) und \(E' + \delta E'\) sind jeweils
mit gleicher Wahrscheinlichkeit besetzt, während alle anderen Mikrozustände nicht erreichbar sind.
Wir vernachlässigen also alle Mikrozustände des Gesamtsystems, bei denen zwar \(E_{n} + E'_{n'}\) ungefähr gleich \(E + E'\) ist, aber \(E_{n}\) außerhalb des Energieintervalls bei \(E\) und entsprechend auch \(E'_{n'}\) außerhalb des Energieintervalls bei \(E'\) sind. Man kann zeigen (siehe kanonisches Ensemble weiter unten), dass solche Energiefluktuationen zwischen makroskopischen Systemen extrem selten sind, wenn die Systeme einzeln annähernd im thermischen Gleichgewicht sind.
Die beiden Systeme A und A' bilden zusammen ein makroskopisch isoliertes Gesamtsystem Ag , das eine Gesamtenergie \[ E_{g} = E + E' \] (mit zugehörigem kleinen Energieintervall) besitzt.
Die Makrozustände dieses Gesamtsystems können wir durch die Makrozustände der beiden Teilsysteme charakterisieren, also durch \( (N, V, E, N', V', E') \). Da sich die Teilchenzahlen und die Volumina nicht ändern sollen, lassen wir sie hier weg und schreiben kurz \( (E, E') \) für den Makrozustand des Gesamtsystems.
Die Angabe der Gesamtenergie \(E_{g}\) genügt also hier nicht, um diesen Gesamt-Makrozustand zu charakterisieren. Daran erkennt man, dass sich das Gesamtsystem aus A und A' noch nicht im thermischen Gleichgewicht befindet. Die Teilsysteme A und A' sind zwar jedes für sich annähernd im thermischen Gleichgewicht und können daher jeweils durch nur einen Energiewert \(E\) und \(E'\) charakterisiert werden, aber sie sind nicht miteinander im Gleichgewicht.
Die Wechselwirkung zwischen A und A' soll nun so gering sein, dass sie die Mikrozustände von A und A' praktisch nicht verändert. Quantenmechanisch bedeutet das, dass wir im Gesamt-Hamiltonoperator \[ \hat{H}_{g} = \hat{H} + \hat{H}' + \hat{H}_{int} \] den Wechselwirkungsanteil \( \hat{H}_{int} \) für die Zustände vernachlässigen können.
Jeder Mikrozustand \( |n_{g}\rangle \) des Gesamtsystems Ag setzt sich dann zusammen aus einem Mikrozustand \( |n\rangle \) von A und einem Mikrozustand \( |n'\rangle \) von A'. Wir schreiben auch \[ |n_{g}\rangle = |n,n'\rangle \] (das kann man als mathematisches Tensorprodukt lesen).
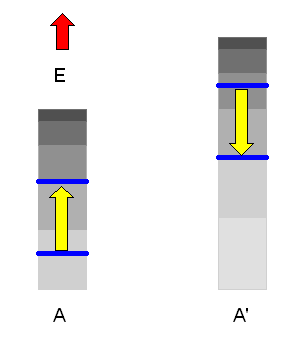
Wenn es nun \(\Omega(E)\) erlaubte n-Werte (erreichbare Zustände) in A und \(\Omega'(E')\) erlaubte n'-Werte in A' gibt, so gehören dazu \(\Omega(E) \cdot \Omega'(E')\) erlaubte Kombinationen von n und n' im Gesamtsystem Ag. Die Zahl der erreichbaren Mikrozustände im Makrozustand \( (E, E') \) des Gesamtsystems ist also das Produkt \[ \Omega_{g}(E,E') = \Omega(E) \cdot \Omega'(E') \] Das Gesamtsystem beginnt nun wieder, im Raum der erreichbaren Mikrozustände herumzuwandern, wobei sich \(E\) und \(E'\) langsam ändern können – die Gesamtenergie \( E_{g} = E + E' \) muss allerdings konstant bleiben (bis auf die übliche kleine Energieunschärfe).
Dadurch werden neue Mikrozustände für das Gesamtsystem zugänglich, die vorher verboten waren. Auf lange Sicht werden sich dann \(E\) und damit auch \(E' = E_{g} - E\) mit extrem großer Wahrscheinlichkeit so einstellen, dass der zugehörige Makrozustand derjenige mit der größten Zustandszahl \(\Omega_{g}(E,E')\) ist. Das System befindet sich dann im thermischen Gleichgewicht.
Dass dieser Gleichgewichtszustand mit extrem hoher Wahrscheinlichkeit erreicht wird,
erkennt man daran, dass
die Funktion \( \Omega_{g}(E,E') \) für ein bestimmtes \(E\)
(und damit ein bestimmtes \(E' = E_{g} - E\) ) ein extrem scharfes Maximum besitzt,
denn sie verhält sich wie
\( E^{N} \cdot (E_{g} - E)^{N} \). Die folgende Grafik zeigt diese
Funktion (mit willkürlicher absoluter Skalierung, \(E_{g} = 1\) und \(E\) entlang der x-Achse)
für \(N = 1, 2, 4\):
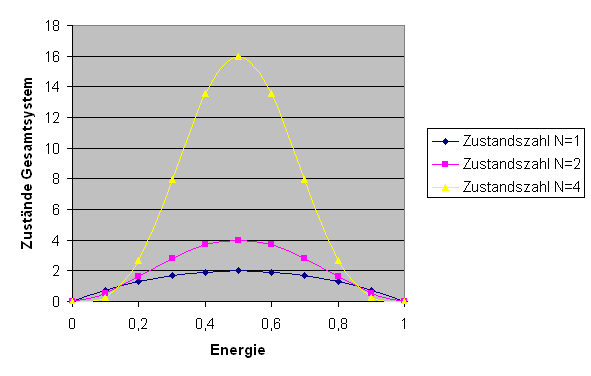
Zahl der Zustände \( \Omega_{g}(E,E') \) im Gesamtsystem für \(N = 1, 2, 4\).
Man kann sich vorstellen, wie scharf das Maximum für \(N = 10^{20}\) wird.
Seine typische Breite beträgt etwa \( \frac{E_{max}}{\sqrt{N}} \)
(die gesamte Rechnung findet man
beispielsweise im Berkeley Physik Kurs, Band 5:
Statistische Physik, Kapitel 4.1.1).
Ein Makrozustand, bei dem \(E\) um mehr als den \(10^{- 10}\)-ten Teil
(also etwa ein Zehntel eines Milliardstels) von \(E_{max}\)
abweicht, ist demnach im thermischen Gleichgewicht bereits sehr unwahrscheinlich.
Den weitaus wahrscheinlichsten Makrozustand finden wir also, indem wir das Maximum von \( \Omega_{g}(E,E') \) suchen. Gleichwertig dazu können wir auch das Maximum von \( k \cdot \ln{\Omega_{g}(E,E')} \) suchen, also das Maximum der Entropie des Gesamtsystems.
Dieses Entropie-Maximum ist wesentlich weniger scharf ausgeprägt als das Maximum von \(\Omega_{g}(E,E')\), da der Logarithmus bei großen Zahlen stark glättend wirkt (siehe die entsprechende Grafik etwas weiter unten). Die Entropie des Gesamtsystems ist dabei gleich der Summe der beiden Entropien der Teilsysteme, wie diese kleine Rechnung zeigt (die Entropie ist also eine sogenannte extensive Größe wie das Volumen): \[ S_{g}(E,E') = \] \[ = k \cdot \ln{\Omega_{g}(E,E')} = \] \[ k \cdot \ln{\left( \Omega(E) \cdot \Omega'(E') \right)} = \] \[ = k \cdot \ln{\Omega(E)} + k \cdot \ln{\Omega'(E')} = \] \[ = S(E) + S'(E') \] Dabei ist immer \( E' = E_{g} - E \) mit vorgegebenem \(E_{g}\), d.h. wir können als einzigen Parameter die Energie \(E\) des ersten Teilsystems wählen und schreiben kurz \[ S_{g}(E) = S(E) + S'(E_{g} - E) \] Das Maximum finden wir, indem wir die Ableitung nach \(E\) gleich Null setzen (dass das wirklich ein Maximum und kein Minimum ist, haben wir oben gesehen, denn \(\Omega_{g}\) hatte ein Maximum): \[ 0 = \frac{dS_{g}(E)}{dE} = \] \[ = \frac{dS(E)}{dE} + \frac{dS'(E_{g} - E)}{dE} = \] \[ = \frac{dS(E)}{dE} - \frac{dS'(E')}{dE'} \bigg|_{E' = E_{g} - E} \] Es muss also im Maximum \[ \frac{dS(E)}{dE} = \frac{dS'(E')}{dE'} \] sein mit der Nebenbedingung \( E' = E_{g} - E \). Die Gleichung sagt:
Offenbar spielt also die Ableitung der Entropie nach der Energie eine besondere Rolle im thermischen Gleichgewicht. Den Kehrwert dieser Ableitung bezeichnet man als Temperatur \(T\) (man nimmt den Kehrwert, damit bei wachsender Energie die Temperatur zunimmt, siehe weiter unten).
|
Die Temperatur \(T\):
Die Temperatur \(T\) eines makroskopischen Systems im thermischen Gleichgewicht bei festem Volumen und fester Teilchenzahl ist definiert als der Kehrwert der Ableitung der Entropie nach der Energie: \[ \frac{1}{T} := \frac{dS(E)}{dE} \] Genauer müsste man \(T(E)\) schreiben, da die Temperatur wie die Entropie natürlich von der Energie des Systems abhängt.
|
Die Bedingung
\[
\frac{dS(E)}{dE} = \frac{dS'(E')}{dE'}
\]
für das thermische Gleichgewicht können wir damit schreiben als
\[
\frac{1}{T(E)} = \frac{1}{T'(E')}
\]
oder kurz als
\[
T = T'
\]
Die Temperaturen der Teilsysteme sind im thermischen Gleichgewicht gleich groß.
Genau das wollten wir haben.
Natürlich können wir \(\frac{1}{T}\) auch durch die Zustandszahl \(\Omega(E)\) ausdrücken: \[ \frac{1}{T} := \frac{dS(E)}{dE} = \] \[ = k \, \frac{d\ln{\Omega(E)}}{dE} = \] \[ = k \, \frac{1}{\Omega(E)} \, \frac{d\Omega(E)}{dE} \] Rechts steht (bis auf einen Vorfaktor) die relative Wachstumsrate der Zustandsanzahl mit der Energie. Man kann auch sagen: Rechts steht (bis auf einen Vorfaktor), wie schnell die Zahl der Stellen der Zustandsanzahl \(\Omega(E)\) mit der Energie zunimmt. Die Temperatur ist dann proportional zur Energiezunahme, die man braucht, um die Stellenzahl um eine weitere Stelle zu erhöhen (d.h. um die Zustandsanzahl zu verzehnfachen). Je höher die Temperatur ist, umso weniger schnell wächst die Zahl der Stellen der Zustandsanzahl mit wachsender Energie an. Anschaulich kann man sich vorstellen, dass die Zustandsanzahl bei hoher Temperatur (und damit hoher Energie) bereits so gigantisch ist, dass das prozentuale Wachstum nicht mehr so groß sein kann.
Woher wissen wir, dass die Temperatur im Normalfall mit wachsender Energie zunimmt? Rechnen wir es mit den Formeln oben (insbesondere \( \phi(E) = B^{N} \, V^{N} \, (E/N)^{b N} \) ) einfach aus, wobei diese Formeln den erwähnten Normalfall charakterisieren sollen: \[ \frac{1}{T} := \frac{dS(E)}{dE} = \] \[ = k \, \frac{d\ln{\Omega(E)}}{dE} = \] \[ = k \, \frac{d \ln{\phi(E)}}{dE} = \] \[ = k \, \frac{1}{\phi(E)} \, \frac{d\phi(E)}{dE} = \] \[ = k \, \frac{1}{E^{bN}} \, b \, N \, E^{bN - 1} = \] \[ = k \, b \, N \, \frac{1}{E} = \] \[ = k \, b \, \frac{1}{\epsilon} \] oder nach der Einteilchenenergie freigestellt: \[ \epsilon = b \, k \, T \] In unserem Gas-Beispiel oben haben wir gesehen, dass bei nur einem Freiheitsgrad pro Gasteilchen (Schwingungen nur in einer Raumrichtung) \(b = 1/2\) ist, bei drei Freiheitsgraden (Raumrichtungen) aber \(b = 3/2\) ist. Wir vermuten, dass allgemein \(b = f/2\) ist mit \(f =\) Zahl der Freiheitsgrade pro Gasteilchen (das wollen wir hier nicht genauer begründen). Dann hätten wir \[ \epsilon = \frac{f}{2} \, k \, T \] Das wollen wir festhalten:
|
Temperatur und Energie pro Freiheitsgrad: Die Temperatur \(T\) eines makroskopischen Systems im thermischen Gleichgewicht mit \(N\) Teilchen und festem Volumen nimmt im Normalfall mit der Energie \(E\) zu. Die mittlere Energie pro Freiheitsgrad ist bei typischen makroskopischen Systemen (z.B. einem ideales Gas) gegeben durch \[ \frac{1}{2} \, k \, T \] Beispielsweise ist die mittlere Energie eines Teilchens mit 3 Freiheitsgraden (entsprechend den Bewegungen in drei Raumrichtungen) gegeben durch \[ \epsilon = \frac{3}{2} \, k \, T \] |
Jetzt wissen wir, warum der Kehrwert \(1/T\) bei der Definition der Temperatur über die Entropie
günstig war, denn so erhält die Temperatur eine sehr anschauliche Bedeutung: sie ist
im Normalfall ein Maß
für die mittlere Energie pro Freiheitsgrad. Die Boltzmannkonstante \(k\) braucht man dabei nur,
da man für die Temperatur historisch die Maßeinheit Kelvin festgelegt hat
und daher Energieeinheiten in Kelvin umrechnen möchte.
Man hätte genauso gut überall in diesem Kapitel \(k\) weglassen können – dann wäre die Entropie einfach eine Zahl (ungefähr 2,3 mal die Stellenzahl der Zustandsanzahl) und die Temperatur würde man direkt in Energieeinheiten angeben. Statt \(T = 300\) Kelvin (etwa Zimmertemperatur) würde man dann direkt \(T = 1/40\) eV sagen und damit sofort wissen, dass die mittlere Bewegungsenergie eines Gasteilchens 3/2 mal dieser Temperatur ist.
Die Tatsache, dass die Temperatur mit wachsender Energie zunimmt, bedeutet, dass ihr Kehrwert und damit die Steigung der Entropie pro Energiezufuhr mit wachsender Gesamtenergie abnimmt. Man sagt auch, die Entropiekurve \(S(E)\) ist konkav, beschreibt also eine Rechtskurve. Genau das haben wir bereits oben in der Entropie-Grafik eines typischen Systems gesehen.
Die Summe von zwei konkaven Kurven ist nun ebenfalls konkav und hat ein Maximum – noch eine Begründung, warum die Gesamtentropie ein Maximum hat. Umgekehrt gilt: Wäre die Entropiekurve nicht konkav (d.h. würde \(1/T\) nicht mit wachsendem \(E\) abnehmen) so gäbe es beim Zusammenbringen zweier solcher Systeme kein Entropiemaximum bei einer bestimmten Energieaufteilung, was zu einer merkwürdigen Situation führt – die Gesamtenergie würde sich komplett in einem der beiden Teilsysteme sammeln.
Übrigens ist die Entropiekurve auch für unser Spinsystem weiter unten konkav, wobei die Temperatur dort bei höheren Energien negativ wird, weil die Entropiekurve dort sogar wieder abfällt. Der heißere Zustand ist aber immer noch derjenige mit dem kleineren Wert von \(1/T\), also mit der kleineren Entropiesteigung. Das funktioniert auch bei negativen Temperaturen. Wir kommen gleich noch genauer darauf zurück.
Die folgende Grafik stellt die Entropiesumme \[ S(E) + S'(E_{g} - E) \] dividiert durch \(k N\) für zwei typische gleich große Systeme bis zu \( E/N = \epsilon = 1/40\) eV dar, was der typischen Teilchenenergie bei Zimmertemperatur entspricht.
Man erkennt schön das recht flache Entropiemaximum. Wer möchte, kann das dargestellte \(S_{g}/(kN)\) auch leicht in die Anzahl Dezimalstellen der Zustandsanzahl umrechnen: \[ \mathrm{Stellenzahl} \, \mathrm{von} \, \Omega_{g} = \] \[ = \log{\Omega_{g}} = \frac{N}{2,3} \, \frac{S}{kN} \] Bei einem Mol wäre \(N = 6 \cdot 10^{23}\) und wir hätten ungefähr: \[ \mathrm{Stellenzahl} \, \mathrm{von} \, \Omega_{g} = \] \[ = \log{\Omega_{g}} = 2 \cdot 10^{23} \, \frac{S}{kN} \] Wenn also in der Grafik das dargestellte \(S_{g}/(kN)\) nur um 0,01 ansteigt, so vergrößert sich die Stellenzahl von \(\Omega_{g}\) um \(2 \cdot 10^{21}\) Dezimalstellen – \(\Omega_{g}\) selbst wächst also um den Faktor \(10^{(2 \cdot 10^{21})}\), was weit mehr ist als die Zahl der Atome im sichtbaren Universum. Das flache Entropiemaximum entspricht also einem extrem scharfen Maximum in der Zustandsanzahl. Man darf sich also von dem flachen Entropiemaximum nicht täuschen lassen! Hier ist die Grafik:
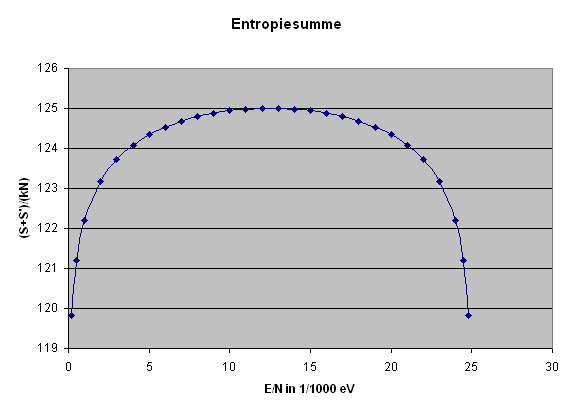
Entropiesumme
\(
S(E) + S'(E_{g} - E)
\)
zweier typischer gleich großer thermisch verbundener Systeme,
dividiert durch \(k N\)
bis zu \( E/N = \epsilon = 1/40\) eV.
Aus der Definition der Temperatur können wir noch einen Zusammenhang zwischen der absorbierten Wärmemenge
\(Q\) und der Entropieänderung \(\Delta S\) eines Systems ablesen.
Dazu nehmen wir an, dass die absorbierte Wärmemenge \(Q\)
so gering ist (oder das System so groß ist), dass sich die
Temperatur praktisch nicht ändert – deshalb schreiben
wir \(\delta Q\) statt \(Q\) (wir schreiben nicht \(dQ\), um anzudeuten, dass man
\(\delta Q\) bei allgemeineren Randbedingungen nicht
als Differenz zweier Zustandsgrößen verstehen kann,
anders als \(dS\) oder \(dE\) – so muss beispielsweise
bei veränderlichem Volumen die Wärmemenge nicht \( \delta Q = -\delta Q' \) erfüllen
– es muss nur \( dE = - dE' \) sein – mehr dazu später).
Außerdem hatten wir vorausgesetzt, dass die Absorption der Wärmemenge \(Q\) sehr langsam (quasistatisch) abläuft, so dass sich das absorbierende System ständig im thermischen Gleichgewicht befindet und jederzeit durch einen Makrozustand \((E, V, N)\) beschrieben werden kann. Die absorbierte Wärmemenge \(\delta Q\) ist in unserem Fall gleich der zufließenden Energiemenge \(dE\), denn die äußeren Parameter (Volumen etc.) sollen ja konstant bleiben, d.h. die Energieniveaus der Mikrozustände ändern sich nicht. Aus \[ \frac{1}{T} = \frac{dS(E)}{dE} \] folgt dann \[ dS = \frac{dE}{T} = \frac{\delta Q}{T} \]
|
Zusammenhang zwischen zufließender Wärmemenge und Entropiezunahme: Ist das absorbierende System im thermischen Gleichgewicht, und ist die absorbierte Wärmemenge \(\delta Q\) so klein, dass sich die Temperatur des Systems praktisch nicht ändert, und erfolgt die Absorption der Wärmemenge so langsam (quasistatisch), dass jederzeit ein thermische Gleichgewicht des Systems gewährleistet ist, so ist die Entropiezunahme des absorbierenden Systems gleich \[ dS = \frac{\delta Q}{T} \] Wir fordern nicht, dass sich das absorbierende System im thermischen Gleichgewicht mit anderen Systemen befinden muss, oder dass die Wärmeabsorption umkehrbar (reversibel) ablaufen muss. |
Das entspricht der klassischen Definition der Entropie,
als man sie noch nicht über die Zustandsanzahl definierte.
Dabei ist die Wärmemenge definiert als die Energiemenge, die bei konstantem Volumen
und konstanter Teilchenzahl quasistatisch durch Wärmefluss hinzukommt.
Wir haben aber die Entropie weiter oben bereits definiert und können daher die Gleichung auch als Definition der Wärmmemenge \(\delta Q\) ansehen. Wächst die Energie eines (im thermischen Gleichgewicht befindlichen) Systems mit Temperatur \(T\) quasistatisch um einen Betrag \(dE\), so bezeichnen wir den Anteil \[ \delta Q := T \, dS \] der mit der Entropieänderung \(dS\) verbunden ist, als Wärmemenge.
Dabei muss die Wärmemenge \( \delta Q \) so klein sein, dass sich die Temperatur \(T\) praktisch nicht ändert. Falls das System sehr groß ist, so kann die Wärmemenge \(\delta Q\) durchaus größere Werte annehmen – dies ist bei einem sogenannten Wärmebad der Fall. Diese Definition werden wir später beibehalten, wenn Volumen oder Teilchen ausgetauscht werden können.
Was geschieht, wenn wir die Bedingung fallen lassen, dass die Wärmeabsorption quasistatisch ablaufen muss, oder dass sich das System überhaupt im thermischen Gleichgewicht befinden muss? Dann können die makroskopischen Zustände nicht mehr ständig durch nur drei Zahlen \((E, V, N)\) beschrieben werden. So kann die absorbierte Energie makroskopisch ungleich verteilt sein. Die Ableitung \(dS/dE\) ist dann nicht mehr sauber definiert, denn \(dS\) hängt zusätzlich noch davon ab, wie sich die absorbierte Energie \(dE\) verteilt. Man kann sich überlegen, dass im Nicht-Gleichgewicht gilt:
| Für ein System, das sich nicht im thermischen Gleichgewicht befindet, das aber dennoch bereits eine ausgeglichene Temperatur \(T\) aufweist, ist \[ dS \gt \frac{\delta Q}{T} \] |
Diese Aussage können wir noch verallgemeinern, und zwar dann,
wenn das System A im Kontakt mit einem großen Wärmebad A' ist
und die Wärme von diesem Wärmebad erhält.
Dabei soll das Wärmebad A' so groß sein, dass seine Temperatur T'
praktisch konstant bleibt und dass der Energiefluss das thermische Gleichgewicht
des Wärmebades nicht stört.
Dann ist nämlich
\[
\Delta S' = \frac{Q'}{T'}
\]
wobei
weder \(\Delta S'\) noch \(Q'\) besonders klein sein müssen.
Nun nimmt die Gesamtentropie zu, d.h. es ist
\[
\Delta S + \Delta S' \gt 0
\]
Freigestellt nach \(\Delta S\) ist dann
\[
\Delta S \gt - \Delta S' = - \frac{Q'}{T'} = \frac{Q}{T'}
\]
wobei wir \( Q = - Q' \) verwendet haben (diese Gleichung gilt
bei unverändertem Volumen und Teilchenzahl, aber auch
bei Volumenaustausch zwischen A und A' bei gleichem Druck \(p = p'\)
oder Teilchenaustausch bei gleichem chemischen Potential \(\mu = \mu'\) ).
In diesem Sinn gilt die obige Gleichung in der Form \[ \Delta S \gt \frac{Q}{T} \] sogar für ein System, das sich nicht im Gleichgewicht und auch nicht auf ausgeglichener Temperatur befindet, das aber mit einem großen Wärmebad der Temperatur \(T\) (Strich weggelassen) in Kontakt ist und von diesem die Wärme erhält.
| Für ein System mit konstantem Volumen und konstanter Teilchenzahl, das sich nicht im thermischen Gleichgewicht befindet und das thermisch mit einem großen Wärmebad der Temperatur \(T\) gekoppelt ist, gilt \[ \Delta S \gt \frac{Q}{T} \] Dabei ist \(Q\) die Wärmemenge, die das System aus dem Wärmebad aufnimmt, und \(T\) ist die Temperatur des Wärmebades. |
Die Formeln enthalten auch den Fall, dass
\(dS \gt 0\) ist, ohne dass überhaupt eine Wärmemenge von außen absorbiert wird.
Ein Beispiel ist unser Gesamtsystem Ag, das aus den beiden Teilsystemen A und A' besteht,
die noch nicht im thermischen Gleichgewicht miteinander sind.
Die Makrozustände dieses Gesamtsystems Ag können wir nicht durch
\( (E_{g}, V_{g}, N_{g}) \) kennzeichnen,
sondern wir müssen \( (E, V, N, E', V', N') \) verwenden.
Die Entropie kann hier anwachsen, ohne dass das Gesamtsystem Wärme von außen absorbiert.
Sie wächst hier durch einen internen Wärmefluss innerhalb des Systems an.
Genau diesen Fall betrachten wir hier ja ständig!
Zurück zu unseren beiden Gasbehältern A und A'. Beide sind jeweils für sich im thermischen Gleichgewicht, aber noch nicht untereinander. Der Energiefluss zwischen ihnen erfolgt so langsam, dass er das innere thermisches Gleichgewicht der beiden Behälter nicht stört – so wollten wir es einrichten.
Die Gleichung \[ dS = \frac{\delta Q}{T} \] gilt also separat für jeden Gasbehälter, und sie bedeutet, dass sich die Gesamtentropie bei dem Energieaustausch \( \delta Q = dE = - dE' \) nach der Formel \[ dS_{g} = dS + dS' = \] \[ = \frac{dE}{T} + \frac{dE'}{T'} = \] \[ = \delta Q \, \left( \frac{1}{T} - \frac{1}{T'} \right) \] ändert. Wenn also beispielsweise Energie von A' nach A fließt (also \(dE = \delta Q \gt 0\) ist), so muss wegen \(dS_{g} \gt 0\) auch \( (1/T - 1/T') \gt 0\) sein, d.h. es ist \[ \frac{1}{T} \gt \frac{1}{T'} \] Das heißere System ist also immer dasjenige mit dem kleineren Wert von \(1/T\), also mit der kleineren Entropiesteigung. Die Energie fließt als Wärme dann vom heißeren zum kühleren System.
Das stimmt auch beim Spinsystem unten, bei dem es negative Temperaturen gibt.
Im Normalfall sind die Temperaturen aber positiv, so dass der heißere Zustand auch die größere Temperatur hat.
Beim Energiefluss von A' nach A wächst nun die Entropie \(S\) schneller an, als \(S'\) schrumpft, denn \(S'\) hat ja den kleineren \(1/T\)-Wert und damit die kleinere Steigung pro Energieänderung.
Insgesamt wächst also die Gesamtentropie \( S_{g} = S + S' \) an. Dabei verändern sich auch \(T\) und \(T'\) langsam, bis sie schließlich gleich werden und \(dS_{g} = 0\) wird. Das thermische Gleichgewicht ist erreicht und es fließen keine makroskopischen Energiemengen mehr.
Schauen wir uns einige Eigenschaften der Temperatur an:
Einen höchsten Temperaturwert gibt es i.a. nicht, denn die mittlere Energie eines Teilchens kann normalerweise beliebig groß werden – das gilt allerdings nicht für Systeme mit einer nach oben begrenzten Energie, beispielsweise magnetische Spins – wir kommen gleich darauf zurück.
Gibt es einen kleinsten Temperaturwert? Bei der Entropie wissen wir es von ganz oben: Der kleinste Entropiewert ist Null – er entspricht einem Makrozustand, der nur einen einzigen Quantenzustand beinhaltet. Das ist der quantenmechanische Grundzustand des Systems, wie er bei der Energie Null vorliegt (wir legen die Energieskala so, dass eine mögliche quantenmechanische Grundzustandsenergie bei Null liegt). Allerdings ist es im Prinzip möglich, dass der Grundzustand entartet ist, d.h. dass es mehrere Zustände mit Grundzustandsenergie gibt. Außerdem stellt sich bei niedrigen Temperaturen das thermische Gleichgewicht nur sehr langsam ein. Es ist also in der Realität durchaus möglich, dass eine kleine Rest-Entropie übrig bleibt – hier kommt es auf Details an.
Auch die Temperatur wird für verschwindende Energie normalerweise Null, wenn man davon ausgeht, dass \(k T\) ungefähr die mittlere Energie eines Teilchens ist. Allerdings muss man hier vorsichtig sein: Die Zahl der Mikrozustände kann in der Nähe des Grundzustandes klein werden, so dass unsere Voraussetzung von einer großen Zustandsanzahl im Energieintervall fraglich wird. Außerdem muss man wieder thermisches Gleichgewicht voraussetzen, was sich bei sehr niedrigen Temperaturen nur sehr langsam einstellt. Deshalb wird es bei sehr kleinen Temperaturen immer schwieriger, die Temperatur noch weiter abzusenken.
Man kann auch direkt mit der Definition der Temperatur argumentieren: \[ \frac{1}{T} = \frac{dS(E)}{dE} = k \, \frac{1}{\Omega(E)} \, \frac{d\Omega(E)}{dE} \] Die Zunahmerate der Zustandsanzahl pro Energiezunahme \( \frac{d\Omega(E)}{dE} \) wird auch in der Nähe des Grundzustandes einen endlichen Wert haben, denn die Zustände haben ja auch dort gewisse definierte Energieabstände.
Die Anzahl der Mikrozustände \(\Omega(E)\) wird jedoch dort sehr viel geringer sein als bei größeren Energien, denn die Teilchen haben nur vergleichsweise wenige Möglichkeiten, die sehr geringen Energie unter sich aufzuteilen (man denke an den Term \(\epsilon^{bN}\), der für große \(N\) und kleine \(\epsilon\) sehr klein wird).
Insgesamt wird also der Term \( k \, \frac{1}{\Omega(E)} \, \frac{d\Omega(E)}{dE} \) auf der rechten Seite nahe der Grundzustandsenergie sehr groß sein, verglichen mit Werten bei höheren Energien.
Entsprechend ist \(1/T\) dort sehr groß bzw. \(T\) sehr klein – man sagt daher, die Temperatur geht gegen Null (absoluter Nullpunkt). Wenn man es aber ganz genau nimmt, ist die Temperatur bei der Grundzustandsenergie nicht wirklich gut definiert, denn man braucht ja zumindest das kleine Energieintervall \(\delta E\).
In den Beispielen oben sind wir immer von normalen makroskopischen Systemen ausgegangen. In solchen Systemen haben Atome immer Freiheitsgrade (Schwingungen, Rotationen oder Translationen), die beliebig viel Energie aufnehmen können.
Es kann aber Situationen geben, in denen wir Freiheitsgrade betrachten, die nicht beliebig viel Energie aufnehmen können. Ein Beispiel sind die Spins von Atomkernen in einem sehr starken Magnetfeld, wie es bei der Kernspintomographie in der Medizin der Fall ist. Diese Kernspins wechselwirken miteinander, haben aber nur eine extrem schwache Wechselwirkung mit den anderen Freiheitsgraden der Atome, so dass wir diese geringe Wechselwirkung vernachlässigen wollen und die Kernspins in dem starken Magnetfeld als eigenes thermodynamisches System betrachten können. Man kann also eine eigene Spin-Entropie und eine zugehörige Spintemperatur für die Kernspins definieren, die nach relativ kurzer Zeit ein Maximum einnimmt (lange bevor die Gesamtentropie des Systems maximal wird).

Im niedrigsten Energieniveau sind alle \(N\) Kernspins parallel zum Magnetfeld ausgerichtet,
d.h. für dieses Energieniveau
gibt es nur einen einzigen Mikrozustand.
Das nächsthöhere Energieniveau hat einen Kernspin umgedreht – dafür gibt es \(N\) Möglichkeiten, also \(N\) Mikrozustände.
Das nächste Energieniveau hat zwei Spins umgedreht – das ergibt \( N \, (N - 1) / 2 \) Zustände. Für das Umdrehen des ersten Spins hat man nämlich wieder \(N\) Möglichkeiten, es bleiben also noch \(N - 1\) Möglichkeiten, anschließend einen zweiten Spin umzudrehen, was zusammen \( N \, (N - 1) \) Möglichkeiten ergibt. Nun ist aber die Reihenfolge, in der wir die beiden Spins umdrehen, egal – wir haben also jede Möglichkeit doppelt erfasst und müssen deshalb noch durch \(2\) dividieren.
Allgemein gibt es \(N\) über \(n\) Möglichkeiten (Zustände), von \(N\) Spins \(n\) Spins umzudrehen (Reihenfolge egal), wobei \(N\) über \(n\) den Binomialkoeffizienten meint.
Die maximale Zustandszahl wird erreicht, wenn die Hälfte der Spins umgedreht ist. Danach werden die Zustände pro Energieniveau wieder weniger, bis man bei dem energetisch höchsten Zustand ankommt, bei dem alle Spins umgedreht sind. Bei einem solchen Spinsystem wächst die Zustandszahl also nicht mit \(E^{N}\) und Formeln wie \( \epsilon = 3/2 \, k \, T \) gelten nicht.
Übrigens haben wir hier einen Fall vor uns, bei dem man das Energieintervall \(\delta E\) gar nicht braucht, denn die einzelnen Energieniveaus sind so stark entartet, dass sie bereits genug Mikrozustände umfassen. Man könnte aber auch gleichwertig dazu sagen: \(\delta E\) wurde gerade so gewählt, dass es der Energie entspricht, die beim Umklappen eines Spins gebraucht wird.
Starten wir mit dem niedrigsten Energiezustand. Wenn man nun Energie in dieses Spinsystem pumpt, so nimmt die Zahl der Mikrozustände pro Energieniveau und damit die Spin-Entropie zunächst zu, bis ein Maximum erreicht wird und sie ab da wieder abnimmt.
Trotzdem ist die Kurve \(S(E)\) immer noch konkav, d.h. die Steigung der Kurve und damit \(1/T\) (Kehrwert der Spintemperatur \(T\)) fällt stetig mit wachsender Energie, wobei die Steigung von positiven Werten schließlich zu negativen Werten übergeht.
Entsprechend startet die Spin-Temperatur \(T\) von Null bis zu immer größeren positiven Werten, wird schließlich Unendlich und wechselt ihr Vorzeichen, um dann bei negativen Werten schließlich wieder Null zu werden.
In diesem Spin-System machen negative Temperaturen also durchaus Sinn, wobei man besser den stetigen Kehrwert \(1/T\) der Temperatur betrachtet.
So wird das thermische Gleichgewicht zwischen zwei solchen Spinsystemen erreicht, wenn sie dieselbe (positive oder negative) Temperatur erreicht haben. Der heißere Zustand ist auch hier derjenige mit dem kleineren Wert von \(1/T\), also mit der kleineren Entropiesteigung. Ein negativer Temperaturwert ist also immer heißer als ein positiver Temperaturwert, denn er hat den kleineren Kehrwert.
Die Energie fließt vom System mit negativer Temperatur zum System mit positiver Temperatur.
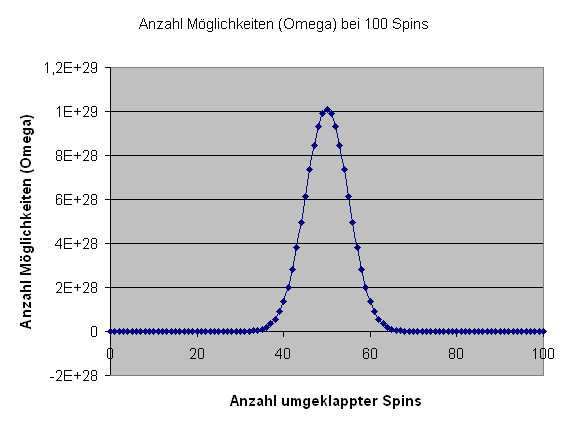
Dargestellt ist hier die Anzahl Möglichkeiten \(\Omega\), \(n\) von \(100\) Spins
auszuwählen und umzuklappen.
Bei etwa 50 umgeklappten Spins hat man die meisten Möglichkeiten.
Da die Energie hier proportional zu \(n\) sein soll, kann man sich die x-Achse auch als Energieachse vorstellen.
Würde man deutlich mehr als nur \(100\) Spins betrachten,
so wäre das Kurvenmaximum deutlich schärfer.
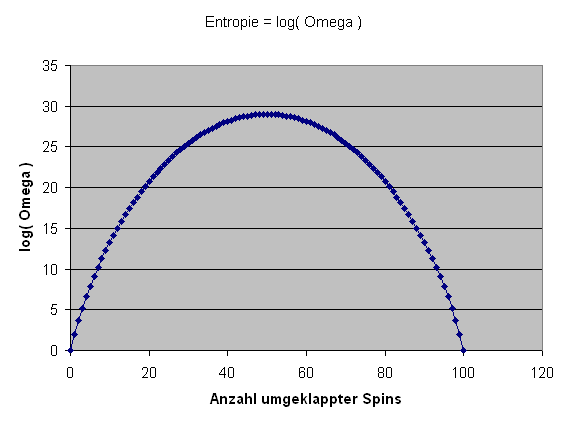
Die Entropie \(S\) des 100-Spin-Systems (hier einfach ohne Vorfaktor
gleich dem Zehnerlogarithmus \( \log{\Omega} \) gesetzt.
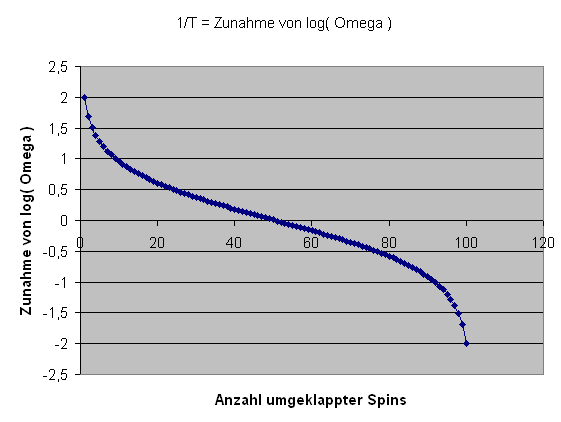
Steigung \( dS/dE = 1/T \) der Entropie des 100-Spin-Systems
(wobei wir pro umgeklapptem Spin eine
Energieeinheit rechnen).
Negative Temperaturen treten bei normalen stabilen Systemen mit Bewegungs-Freiheitsgraden der Teilchen dagegen
normalerweise nicht auf.
Diese Freiheitsgrade können nämlich beliebig große Energiemengen aufnehmen, so dass es bei wachsender
Gesamtenergie immer mehr Möglichkeiten gibt, diese Energie unter den Teilchen aufzuteilen.
Die Entropie wächst also bei steigender Energie und ihre Steigung ist damit positiv.
Oben haben wir zwei Systeme miteinander in einen thermischen Kontakt gebracht, so dass sie Energie austauschen können, ohne dass sich äußere Parameter ändern. Insbesondere bleiben Volumen und Teilchenzahl jeweils konstant.
Das wollen wir jetzt ändern: Ein Energieaustausch soll jetzt nur möglich sein, indem sich das Volumen der Teilsysteme ändert. Wir können uns zwei Gasbehälter vorstellen, zwischen denen sich eine frei bewegliche, aber thermisch gut isolierte Wand befindet. Wärme und Teilchen können nicht durch diese Wand dringen, aber die Wand kann sich verschieben, wobei keine Reibung auftreten soll. Die beiden Teilsysteme A und A' können gleichsam Volumen austauschen. Das macht natürlich besonders bei Gasen Sinn, weniger bei Flüssigkeiten oder Festkörpern.
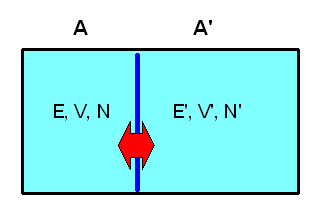
Bei der Volumenänderung ändern sich die Energieniveaus der Mikrozustände, wobei sich deren Besetzungswahrscheinlichkeiten \(P_{n}\) und \(P_{n}'\) nicht ändern. Der Energieaustausch zwischen den Systemen findet hier also alleine durch die Veränderung der Energieniveaus der Mikrozustände statt. Den entsprechenden Energiezuwachs eines Systems bezeichnet man als die an dem System verrichtete makroskopische Arbeit \(W\), im Unterschied zur Wärmemenge oben:
|
Die Arbeit \(W\): Ändert sich bei einem makroskopischen Systemen ein äußerer Parameter (beispielsweise das Volumen), ohne dass eine Wärmemenge oder Teilchen absorbiert werden, so ändern sich dadurch die Energieniveaus der Mikrozustände, ohne dass sich deren Wahrscheinlichkeiten ändern. Die dadurch aufgenommene Energiemenge \(\Delta E\) bezeichnet man als die am System verrichtete Arbeit \(W\), d.h. in diesem Fall ist \[ \Delta E = W \] |
Es wäre nun naheliegend, analog zu oben vorzugehen und das Maximum der Gesamtentropie
bei langsamen Änderungen der Volumenverteilung ohne Wärmefluss
zu suchen, um den thermischen Gleichgewichtszustand zu bestimmen.
Dabei gibt es aber ein Problem: Die Entropie der Teilsysteme und damit des Gesamtsystems
ändert sich hier gar nicht! Man nennt einen solchen Prozess adiabatisch.
Am einfachsten sieht man das, wenn man sich vorstellt, dass der Makrozustand nur ein einziges stark entartetes Energieniveau mit Energie \(E = E_{n}\) umfasst, das aus \(\Omega(E)\) Quantenzuständen besteht. Verändert man nun das Volumen, so verschiebt sich nur die Lage dieses besetzten Niveaus bei unveränderter Zustandsanzahl, d.h. der Makrozustand umfasst immer noch dieselbe Anzahl Mikrozustände wie zuvor.
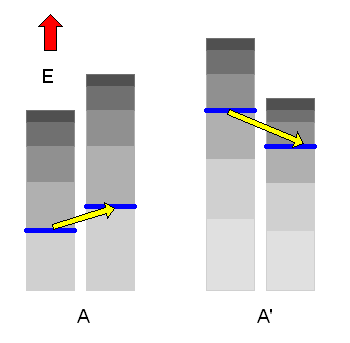
Nun bedeutet konstante Entropie nicht, dass sich in dem System nichts tut.
So könnte die bewegliche Wand reibungslos hin- und herschwingen, wobei Energie
zwischen den beiden Teilsystemen hin- und herwandert – die Wandbewegung muss dabei so langsam sein,
dass beide Teilsysteme jeweils für sich im thermischen Gleichgewicht bleiben.
Man sieht: Der adiabatische Prozess ist thermodynamisch umkehrbar (reversibel), d.h. die Wand kann wie ein Pendel reibungsfrei vor- und zurückschwingen. Konstante Entropie bedeutet dabei, dass sich kein thermisches Gleichgewicht einstellt (wenn man es nicht schon hat). So etwas wie Reibungseffekte gibt es bei einem adiabatischen Prozess nicht.
Übrigens: Adiabatisch bedeutet mehr als nur reversibel, denn die Entropie der Teilsysteme soll bei dem Prozess konstant bleiben (die Teilsysteme sind also jeweils im thermischen Gleichgewicht und dabei voneinander wärmeisoliert). Bei einem reversiblen Prozess genügt es dagegen, dass die Gesamtentropie konstant bleibt.
Anmerkung:
Streng reversible Prozesse gibt es in der Natur nicht, denn
jeder real ablaufende Prozess ist mit einer (vielleicht geringen) zeitlichen Entropiezunahme
verbunden. Reversible Prozesse stellen einen idealisierten Grenzfall dar, bei dem der Prozess
unendlich langsam ablaufen muss. Genau genommen ist ein reversibler Prozess
eine kontinuierliche Aneinanderreihung von Gleichgewichtszuständen,
bei der es aber keine bevorzugte Zeitrichtung gibt. Man kann nicht sagen, in welche Zeitrichtung
ein reversibler Prozess ablaufen muss (wie das Wort reversibel auch sagt).
Ein realer (irreversibler) Prozess setzt immer ein gewisses Ungleichgewicht voraus,
das durch den Prozess ausgeglichen wird.
Schreibt man die Entropie \(S\) als Funktion von \(E\) und \(V\) (Die Teilchenzahl \(N\) lassen wir noch weg, da es hier konstant ist), so bedeutet der obige adiabatische Prozess: \(E\) verändert sich gerade so mit \(V\), dass \(S(E,V)\) konstant bleibt. Man kann daher die an einem System verrichtete Arbeit \(W\) von der absorbierten Wärmemenge \(Q\) so abgrenzen:
Unterschied von Arbeit und Wärmemenge:
|
Normalerweise hat man einen gemischten Fall vor sich, bei dem
die Wand beweglich und zugleich wärmedurchlässig ist.
Außerdem tritt bei der Wandbewegung normalerweise Reibungswärme auf, die sich irgendwie im System verteilt.
In diesem Fall setzt sich die von einem System aufgenommene Energie \(\Delta E\)
aus einer Wärmemenge \(Q\) und der am System verrichteten Arbeit \(W\) zusammen,
d.h. die Volumenänderung verschiebt die Energieniveaus \(E_{n}\) der Mikrozustände
und zusätzlich ändern sich deren Besetzungswahrscheinlichkeiten \(P_{n}\).
Das nennt man den ersten Haupsatz der Thermodynamik:
| Erster Hauptsatz der Thermodynamik (ohne Teilchenaustausch): \[ \Delta E = W + Q \] |
Dieser Satz gilt immer, auch ohne thermisches Gleichgewicht.
Im Grunde ist dieser Satz gleichwertig zum Energieerhaltungssatz,
wenn man weiß, dass Zuführung von Wärme auch eine Form der Energieübertragung ist.
Bei Teilchenaustausch kommt noch ein weiterer Term \(W_{N}\) hinzu, der die Energieänderung
aufgrund eines Teilchenstroms darstellt.
Im gemischten Fall mit wärmedurchlässiger beweglicher Wand ohne Teilchenaustausch macht es wieder Sinn, das Maximum der Entropie zu suchen, denn hier kann man \(E\) und \(V\) als voneinander unabhängige Variablen betrachten und ihren Einfluss auf die Entropie \(S(E,V)\) getrennt untersuchen. Eine Änderung in \(V\) muss nun nicht mehr unbedingt zu einer Änderung in \(E\) führen, denn ein Wärmefluss kann die verrichtete Arbeit ja ausgleichen und so \(E\) konstant halten. Die absorbierte Wärmemenge führt dann letztlich zur Entropiezunahme – mehr dazu etwas weiter unten.
Ändern sich \(E\) und \(V\) nur wenig, so können wir (bei quasistatischen Prozessen und einem System im thermischen Gleichgewicht) eine kleine Entropieänderung schreiben als: \[ dS(E,V) = \frac{\partial S}{\partial E} \, dE + \frac{\partial S}{\partial V} \, dV \] wobei hier jeweils die partiellen Ableitungen der Funktion \(S(E,V)\) nach den voneinander unabhängigen Variablen \(E\) und \(V\) gemeint sind (daher das geschwungene \(\partial\)). Das haben wir weiter oben noch nicht so streng gesehen, da wir dort immer nur eine Variable betrachtet hatten.
\(\frac{\partial S}{\partial E}\) meint also die Ableitung bei konstantem \(V\) und \(\frac{\partial S}{\partial V}\) die Ableitung bei konstantem \(E\) (\(N\) ist hier sowieso noch konstant).
Hier können wir die Definition der Temperatur \[ \frac{\partial S}{\partial E} = \frac{1}{T} \] (bei konstantem \(V\), daher jetzt zur Verdeutlichung klar als partielle Ableitung geschrieben) einsetzen und erhalten \[ dS(E,V) = \frac{dE}{T} + \frac{\partial S}{\partial V} \, dV \] (die Änderungen sollen so klein sein, dass die Temperatur \(T\) als konstant angesehen werden kann).
Wir könnten uns nun direkt für \(\frac{\partial S}{\partial V}\) interessieren, analog zu \(\frac{\partial S}{\partial E}\). Es ist jedoch nützlich, hier noch die Temperatur herauszuziehen und den Druck so zu definieren:
|
Der Druck \(p\): Der Druck \(p\) eines makroskopischen Systems im thermischen Gleichgewicht bei konstanter Energie \(E\) und konstanter Teilchenzahl \(N\) ist definiert als die partielle Ableitung \[ \frac{p}{T} := \frac{\partial S(E,V)}{\partial V} \] |
Warum das in dieser Form nützlich ist, sehen wir beim Einsetzen:
\[
dS(E,V) = \frac{dE}{T} + p \, \frac{dV}{T}
\]
Jetzt hat nämlich \(p \, dV \) die Dimension einer Energie und wir können mit \(T\) multiplizieren
sowie nach \(dE\) freistellen:
\[
dE = T \, dS - p \, dV
\]
Dabei müssen wir \(E\) als Funktion von zwei unabhängigen Variablen
\(S\) und \(V\) sehen: \( E = E(S,V) \). Man stellt
gleichsam die Formel \( S = S(E,V) \) nach \(E\) frei und erhält damit \(E\) als
Funktion von \(S\) und \(V\) (warum das geht, kommt gleich).
Entsprechend ist \[ dE = \frac{\partial E}{\partial S} \, dS + \frac{\partial E}{\partial V} \, dV \] (partielle Ableitungen!) und somit (Vergleich mit oben) \[ T = \frac{\partial E}{\partial S} \] (bei konstantem \(V\), den Kehrwert davon kennen wir schon) und \[ p = - \frac{\partial E}{\partial V} \] (bei konstantem \(S\), also ohne Wärmefluss).
Eine kleine Energieänderung \(dE\) eines Systems können wir also (bei fester Teilchenzahl) in zwei Anteile aufteilen:
|
Erster Hauptsatz im Detail (ohne Teilchenaustausch):
\[ dE = \delta Q + \delta W \] Bei einem System im thermischen Gleichgewicht und einer quasistatischen Energieänderung \(dE\) gilt zusätzlich: \[ \delta Q = T \, dS \] ist die vom System absorbierte Wärmemenge bei konstantem \(V\) und sich ändernder Entropie (also ohne Wärmeisolierung). Dabei ist \[ T = \frac{\partial E}{\partial S} \] (partielle Ableitung, also bei konstantem \(V\)). Bei einem System im thermischen Gleichgewicht und einer quasistatischen Energieänderung \(dE\) gilt außerdem: \[ \delta W = - p \, dV \] ist die am System verrichtete Arbeit bei konstanter Entropie (also mit Wärmeisolierung) und sich änderndem Volumen. Das negative Vorzeichen bedeutet, dass die Energie wächst, wenn das Volumen bei positivem Druck zusammengedrückt wird (\(dV\) also negativ ist). Dabei ist \[ p = - \frac{\partial E}{\partial V} \] (partielle Ableitung, also bei konstantem \(S\)).
|
Wie oben bereits erwähnt, sind \(\delta Q\) und \(\delta W\) (anders als \(dS\) oder \(dE\))
keine Differenzen von Zustandsgrößen, d.h. man kann nicht von der Wärme oder der Arbeit
eines Körpers sprechen, wohl aber von seiner Energie oder Entropie.
Stattdessen kennzeichnen \(\delta Q\) und \(\delta W\) verschiedene Möglichkeiten, wie eine Energie \(dE\) aufgenommen werden kann: durch Umbesetzung der mikroskopischen Energieniveaus oder durch Verschiebung dieser Energieniveaus.
Mathematisch kann man durchaus Integrale über \(\delta Q\) und \(\delta W\) bilden – das Ergebnis hängt aber vom Weg ab, den das System dabei in den thermodynamischen Zustandsgrößen beschreibt. Das meint man, wenn man sagt, \(\delta Q\) und \(\delta W\) sind keine vollständigen Differentiale.
Man kann es auch mit Differentialformen ausdrücken (siehe Gekrümmte Räume, Kapitel 11): Es gibt keine Stammform \(Q\) oder \(W\), so dass \(\delta Q = dQ\) oder \(\delta W = dW\) wäre. Oben war \(Q\) ja auch einfach eine große Wärmemenge, die absorbiert wurde, also ein großes \(\delta Q\).
Nun zu der versprochenen Begründung, warum man die Formel \[ S = S(E,V) \] nach \(E\) freistellen kann und eine Formel \[ E = E(S,V) \] daraus erhält:
Das funktioniert natürlich nur, wenn bei festem \(V\) der Zusammenhang zwischen \(E\) und \(S\) eindeutig (bijektiv) ist. Bei normalen Systemen mit positiver Temperatur ist (bei konstantem Volumen) wachsende Energie mit wachsender Entropie verbunden und umgekehrt, denn \[ T = \frac{\partial E}{\partial S} \gt 0 \] In diesem Fall ist der Zusammenhang zwischen \(E\) und \(S\) eindeutig und wir können \( E = E(S,V) \) schreiben. Anders bei unserem Spinsystem oben: Hier muss man sorgfältiger vorgehen und die beiden Bereiche mit positiver und negativer Temperatur unterscheiden – entsprechend gelten die obigen Formeln für das Spinsystem im Allgemeinen nicht ohne weitere Überlegungen.
Zurück zum thermischen Gleichgewicht zwischen den beiden Teilsystemen A und A', wenn sowohl Energie- als auch Volumenaustausch möglich ist. Die Gesamtentropie muss hier ein Maximum haben, um ein thermisches Gleichgewicht zu ermöglichen, d.h. des muss im thermischen Gleichgewicht gelten (wobei wir \(dE' = - dE\) und \(dV' = - dV\) verwenden): \[ 0 = dS_{g} = dS + dS' = \] \[ = \frac{dE}{T} + p \, \frac{dV}{T} + \frac{dE'}{T'} + p' \, \frac{dV'}{T'} = \] \[ = \frac{dE}{T} + p \, \frac{dV}{T} - \frac{dE}{T'} - p' \, \frac{dV}{T'} = \] \[ = dE \, \left( \frac{1}{T} - \frac{1}{T'} \right) + dV \, \left( \frac{p}{T} - \frac{p'}{T'} \right) \] Diese Gleichung soll für beliebige (kleine) \(dE\) und \(dV\) gelten. Für \(dV = 0\) folgt sofort \(T = T'\), so wie wir das oben ja bereits bei konstantem Volumen hergeleitet haben – die Temperaturen müssen im thermischen Gleichgewicht gleich sein.
Setzen wir dies ein, so folgt bei \(dE = 0\) direkt \(p' = p'\), d.h. auch die Drücke müssen gleich sein.
Das Maximum der Zustandsanzahl des Gesamtsystems ist wie bei der Energie \(E\) auch beim Volumen \(V\) wieder sehr scharf ausgeprägt, denn die Volumenabhängigkeit von \( \Omega_{g}(E,V,E',V') \) ist bei konstantem \(E,E'\) und typischen Systemen (speziell beim idealen Gas) proportional zu \[ V^{N} \, V'^{N} = V^{N} \, (V_{g} - V)^{N} \] Relative Druckschwankungen von mehr als \(10^{- 10}\) Anteilen sind bei \(10^{20}\) Teilchen also sehr unwahrscheinlich.
Man kann die Gleichgewichtsbedingung auch direkt aus der Energie ableiten, wobei wir verwenden, dass die Gesamtentropie im thermischen Gleichgewicht konstant ist (es ist also \(dS' = - dS\) ). Außerdem ist natürlich wieder \(dV' = - dV\) (das Gesamtvolumen soll ja konstant sein). Da unser Gesamtsystem abgeschlossen und isoliert sein soll, darf sich die Gesamtenergie makroskopisch nicht ändern. Es muss also gelten: \[ 0 = dE_{g} = dE + dE' = \] \[ = T \, dS - p \, dV + T' \, dS' - p' \, dV' = \] \[ = (T - T') \, dS - (p - p') \, dV \] Diese Gleichung muss wieder für alle kleinen Volumen- und Entropieänderungen gelten, d.h. es folgt \(T = T'\) und \(p = p'\).
Die Bedingung \( dE_{g} = 0 \) kann man nun auch etwas anders interpretieren:
Man betrachtet verschiedene gleichartige Systeme mit verschiedener Gesamtenergie \(E_{g}\), aber gleichem Gesamtvolumen \(V_{g}\) und gleicher Gesamtentropie \(S_{g}\) (und gleicher Teilchenzahl \(N_{g}\)). Diese Systeme sollen wieder jeweils in gleicher Weise aus zwei Teilsystemen A und A' bestehen.
Die Gesamtenergie \(E_{g}\) hängt nun davon ab, wie sich \(S_{g}\) und \(V_{g}\) im Einzelfall auf die beiden Teilsysteme aufteilen. Dasjenige System, das sich im termischen Gleichgewicht befindet, weist dann die geringste Gesamtenergie \[ E_{g} = E(S,V) + E'(S_{g} - S, V_{g} - V) \] auf, und \( dE_{g} = 0 \) kennzeichnet dieses Minimum.
Dass es sich um ein Energie-Minimum handelt, kann man sich am obigen Beispiel des Gasbehälters überlegen:
Setzt man vereinfacht \(b = 1\), so ist \[ S = k \, N \ln{( B \, V \, E / N )} \] Freigestellt nach \(E\) haben wir also \[ E = \frac{N}{B \, V} \, e^{\frac{S}{k N}} \] Damit ist \[ E_{g} = E + E' = \] \[ = \frac{1}{B} \, \left( \frac{N}{V} \, e^{\frac{S}{k N}} + \frac{N'}{V_{g}-V} \, e^{\frac{S_{g}-S}{kN}} \right) \] Bei fester Entropie \(S\) ist die Volumenabhängigkeit von \(E\) also gleich \[ \frac{a}{V} + \frac{a'}{V_{g}-V} \] so dass bei kleinem \(V\) der erste Term groß wird, bei \(V \rightarrow V_{g}\) dagegen der zweite Term – dazwischen liegt ein Minimum.
Analog ist es bei festem Volumen \(V\): Auch hier hat \(E_{g}\) für irgendein \(S\) zwischen \(0\) und \(S_{g}\) ein Minimum. Beispielsweise hat die Funktion \( e^{S} + e^{1 - S} \) bei \(S = 0\) und \(1\) den Wert \( 1 + e = 3,7 \), in der Mitte bei \(S = 1/2\) dagegen den Wert \(2 \, e^{1/2} = 3,3 \). Kein sehr scharfes Minimum, aber immerhin ein Minimum.
Es ist sehr lehrreich, sich genauer anzusehen, wie das thermische Gleichgewicht durch Druckausgleich entsteht. Dazu wollen wir uns einen Zustand ansehen, bei dem zwar die Temperatur zwischen beiden Teilsystemen bereits ausgeglichen ist, aber links noch mehr Druck als rechts herrscht, so dass \(p \gt p'\) ist. Die Zwischenwand soll (mit Reibung) langsam beweglich und wärmedurchlässig sein, so dass die Temperatur auf beiden Seiten ständig gleich bleibt: \(T = T'\). Teilchen können die Wand nicht durchdringen.
Die Druckdifferenz führt nun zu einem Volumenaustausch \( dV = - dV' \), d.h. die Wand bewegt sich (ganz langsam). Außerdem ist ein allgemeiner Energiefluss \( dE = - dE' \) möglich, denn die Zwischenwand ist ja wärmedurchlässig.
Die Gesamtentropie ändert sich also nach der Formel \[ dS_{g} = dS + dS' = \] \[ = \frac{dE}{T} + p \, \frac{dV}{T} + \frac{dE'}{T} + p' \, \frac{dV'}{T} = \] \[ = \frac{dV}{T} \, (p - p') \] Wenn also \(p \gt p'\) ist, dann muss \(dV\) positiv sein, denn \(dS\) muss für das abgeschlossene Gesamtsystem ja positiv sein. Das Volumen \(V\) vergrößert sich also, während \(V'\) schrumpft. Der höhere Druck links schiebt die Wand langsam nach rechts, bis \(p = p'\) wird.
Wie sieht der Energiefluss dabei aus? Allgemein ist \[ dE = \delta Q + \delta W \] \[ dE' = \delta Q' + \delta W' \] Die Gleichung \( dE = - dE' \) ergibt \[ \delta Q + \delta W = - \delta Q' - \delta W' \] oder umgestellt \[ \delta Q + \delta Q' = - \delta W - \delta W' \] In unserem Fall mit \(T = T'\) ist dann \[ \delta Q + \delta Q' = T \, dS + T \, dS' = T \, dS_{g} \] \[ - \delta W - \delta W' = p \, dV + p' \, dV' = (p - p') \, dV \] so dass wir insgesamt wieder \[ T \, dS_{g} = (p - p') \, dV \] erhalten – das hatten wir uns oben schon überlegt.
Aber die Formeln zeigen noch mehr: Da \(dS_{g}\) positiv sein muss, ist auch \( \delta Q + \delta Q' \) positiv – es kann also hier nicht \( \delta Q = - \delta Q' \) sein (anders als im Fall ohne Volumenaustausch). Analog ist es mit \(\delta W\) und \(\delta W'\). Das bedeutet:
Die Wärmemenge, die ein Teilsystem verlässt, muss bei veränderlichem Volumen nicht genauso groß wie die Wärmemenge sein, die das andere Teilsystem erhält. Dasselbe gilt für die Arbeit. Es gibt keine Wärmemenge oder Arbeit des Systems, nur eine Gesamtenergie. Entsprechend gibt es auch i.a. keinen Wärmefluss oder Arbeitsfluss, nur einen Energiefluss.
Noch etwas sehen wir: In der Formel \[ \delta Q + \delta Q' = (p - p') \, dV \] können wir die rechte Seite als die vom System geleistete Arbeit ansehen. Diese wird (beispielsweise durch Reibung bei der Wandbewegung) komplett in Wärme umgewandelt und in Form der Wärmemengen \(\delta Q\) und \(\delta Q'\) den beiden Teilsystemen zugeführt, was dann zur Entropieerhöhung \(T \, dS_{g}\) führt.
Bisher waren die Teilchenzahlen \(N\) und \(N'\) in den beiden Teilsystemen immer konstant vorgegeben (wir beschränken uns auf eine Teilchensorte). Wir können die obige Betrachtung aber nun leicht verallgemeinern und auch einen Teilchenaustausch zwischen den Teilsystemen zulassen, also \(N\) als variabel betrachten und \(N' = N_{g} - N\) mit festem \(N_{g}\) setzen. So könnte unsere bewegliche wärmedurchlässige Wand beispielsweise porös sein.
Es bietet sich an, die Teilchenzahl wie eine kontinuierliche Variable zu behandeln. Bei so vielen Teilchen kommt es ja nicht so genau darauf an. Auch bei der Dichte eines Gases arbeitet man gerne so, d.h. man vergisst die Teilchenstruktur und stellt sich das Gas gleichmäßig über das Volumen verschmiert vor.
Wie wirkt sich eine Änderung der Teilchenzahl auf die Entropie aus? Beim Gasbehälter hatten wir ungefähr \[ S = k \, N \ln{(B \, V \, E / N) } \] (mit \(b=1\)), wobei im Logarithmus eine große Zahl steht. Verändert man \(N\) nun um einen kleinen Wert \(dN\) (beispielsweise um \(1\)), so merkt der Logarithmus davon praktisch nicht. In erster Näherung wäre also \(dS\) proportional zu \(dN\) (bei konstantem \(E\) und \(V\)). Den Proportionalitätsfaktor schreiben wir als \( - \mu / T \) und nennen \(\mu\) das chemische Potential.
Um es etwas präziser zu machen, wiederholen wir einfach die Diskussion, die wir beim Druck kennengelernt haben:
Die Entropie \(S\) betrachten wir im thermischen Gleichgewicht als eine Funktion der Energie \(E\), des Volumens \(V\) und der Teilchenzahl \(N\). Ändern sich \(E, V\) und \(N\) unabhängig voneinander nur wenig und zudem noch quasistatisch, so können die zugehörige kleine Entropieänderung schreiben als \[ dS(E,V,N) = \] \[ = \frac{\partial S}{\partial E} \, dE + \frac{\partial S}{\partial V} \, dV + \frac{\partial S}{\partial N} \, dN \] wobei hier jeweils die partiellen Ableitungen der Funktion \(S(E,V,N)\) nach den voneinander unabhängigen Variablen \(E, V, N\) gemeint sind. Mit den Definitionen \[ \frac{\partial S}{\partial E} =: \frac{1}{T} \] \[ \frac{\partial S}{\partial V} =: \frac{p}{T} \] \[ \frac{\partial S}{\partial N} =: - \frac{\mu}{T} \] ergibt sich
| \[ dS = \frac{dE}{T} + p \, \frac{dV}{T} - \mu \, \frac{dN}{T} \] |
Jetzt hat auch \( \mu \, dN \) die Dimension einer Energie und wir können mit \(T\) multiplizieren sowie nach \(dE\) freistellen:
| \[ dE = T \, dS - p \, dV + \mu \, dN \] |
wobei wir \(E\) als Funktion von \(S, V\) und \(N\) sehen: \[ E = E(S,V,N) \] Halten wir fest:
|
Das chemische Potential \(\mu\): Das chemische Potential \( \mu \) eines makroskopischen Systems im thermischen Gleichgewicht bei konstanter Energie \(E\) und konstantem Volumen \(V\) ist definiert als die partielle Ableitung \[ \frac{\mu}{T} := - \frac{\partial S(E,V,N)}{\partial N} \] Bei konstanter Entropie und konstantem Volumen ist \[ \mu = \frac{\partial E}{\partial N} \] d.h. das chemische Potential gibt an, wie die Energie im thermischen Gleichgewicht bei langsam wachsender Teilchenzahl und konstanter Entropie zunimmt (ist also der Energiezuwachs pro neuem Teilchen).
|
Im thermischen Gleichgewicht muss dann wieder \(\mu = \mu'\) gelten.
Schauen wir uns analog zum Druck wieder an, wie dieses Gleichgewicht entsteht. Dazu wollen wir uns diesmal einen Zustand ansehen, bei dem zwar die Temperatur zwischen den beiden Teilsystemen bereits ausgeglichen ist, aber rechts noch wesentlich mehr Teilchen als links sind, so dass \(\mu' \gt \mu\) ist. Die Zwischenwand soll unbeweglich sein (Druck spielt also keine Rolle), aber sie soll für einzelne Teilchen sowie für Wärme durchlässig sein (also wärmeleitend und diffusionsoffen), so dass die Temperatur auf beiden Seiten gleich bleibt: \(T = T'\). Welche Richtung hat nun der Teilchenfluss?
Die Gesamtentropie ändert sich bei einem Teilchenfluss \( dN = - dN' \) und einem möglichen zusätzlichen Energiefluss \( dE = - dE' \) nach der Formel \[ dS_{g} = dS + dS' = \] \[ = \frac{dE}{T} - \mu \, \frac{dN}{T} + \frac{dE'}{T} - \mu' \, \frac{dN'}{T} = \] \[ = - \frac{dN}{T} \, (\mu - \mu') \] Wenn also \(\mu' \gt \mu\) ist, dann muss \(dN\) positiv sein, denn \(dS_{g}\) muss für das abgeschlossene Gesamtsystem ja positiv sein. Es fließen also langsam Teilchen von Teilsystem A' nach A.
Der Teilchenfluss erfolgt also von größerem zu kleinerem chemischen Potential.
Dies war der Grund dafür, oben zu sagen, dass sich rechts mehr Teilchen befinden. Langsam verändern sich durch den Teilchenfluss auch \(\mu\) und \(\mu'\), bis sie schließlich gleich werden und \(dS_{g} = 0\) wird. Das thermische Gleichgewicht ist erreicht. Dabei werden auch \(dS\) und \(dS'\) gleich Null, d.h. \(dN\) wird Null – es fließen keine Teilchen mehr.
Was den Energiefluss betrifft, so können wir die Diskussion von oben bei Volumenaustausch direkt übernehmen, wobei wir diesmal \[ \delta W = \mu \, dN \] \[ \delta W' = \mu' \, dN' \] setzen. Der Druck \(p\) wird also durch \(- \mu\) ersetzt, und \(dV\) durch \(dN\). Wieder sind die Wärmemengen und die Arbeitsmengen der beiden Systeme nicht entgegengesetzt gleich, und wieder wird die vom System geleistete chemische Arbeit in Wärme umgewandelt, was zur Entropiezunahme führt.
⟹ Weiter zu Kapitel 1b: Was ist Entropie? (Teil 2)
Literatur:
© Jörg Resag, www.joerg-resag.de
last modified on 28 November 2023